基于全相位幅頻特性補償的FIR濾波器設計

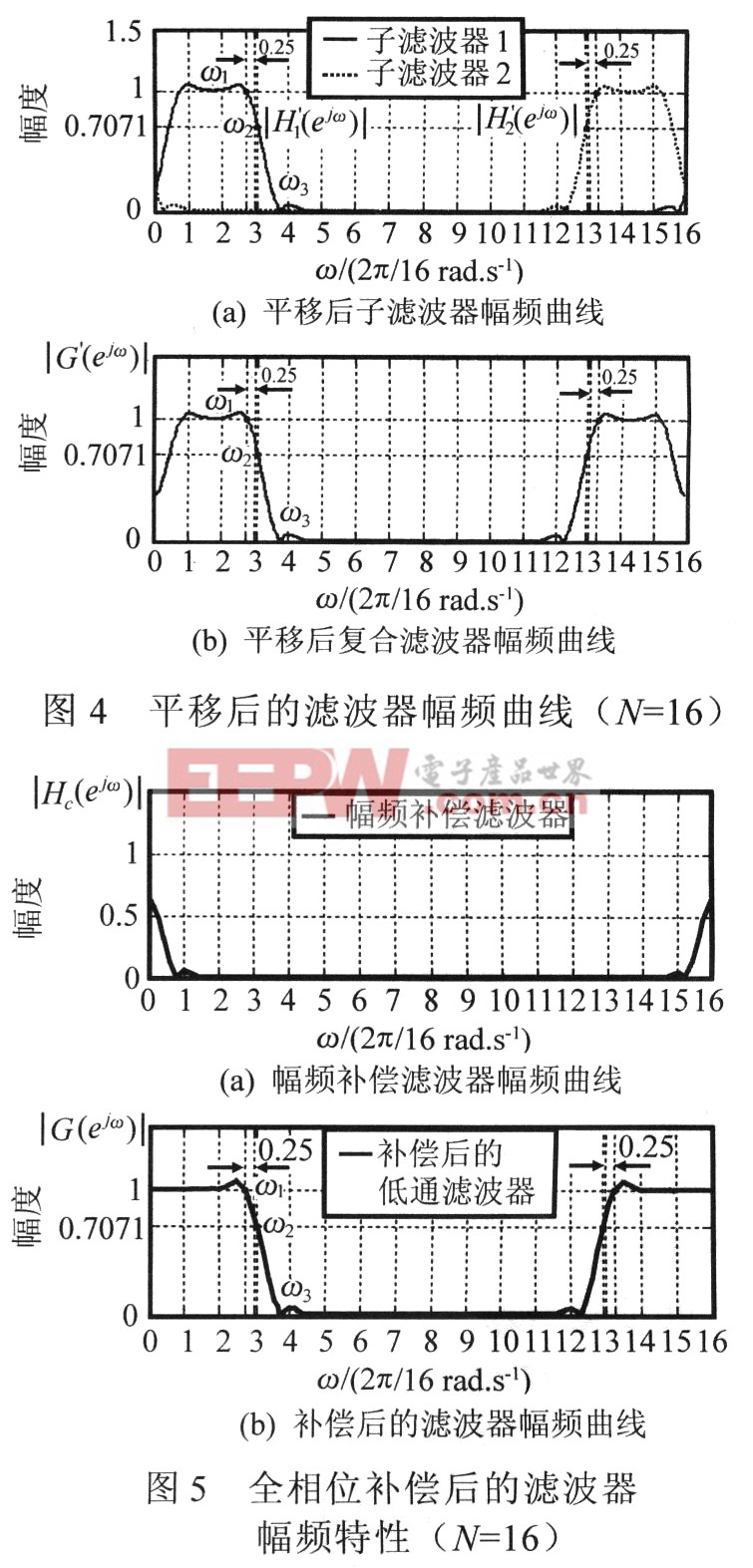
從圖2可看出：|H(ejω)|曲線在通帶內和阻帶內均較平緩，且嚴格通過通帶邊界頻率采樣點ω1=2．5△ω和阻帶邊界頻率采樣點ω3=3．5△ω，這樣就可把過渡帶嚴格控制在頻率采樣問隔△ω內。另外，還可發現，頻率采樣點ωl與ω3間的曲線的線性度很好(N越大時，線性度越好，其線性程度還可通過窗函數進行調節)，若近似把這段曲線看成是直線段，則可估計3dB截止頻率ω2的大致位置為ω2*=(3．5-0．7071)△ω=2．792△ω=1．097(rad．s-1)，實際圖2中ω2=2．839△ω=1．115(rad．s-1)，兩者存在0．018(rad．s-1)的微小差別，增大N或者選擇一個好的窗函數可將此差別減小。
以下通過幅頻特性補償法，可實現圖2的邊界頻率ωl、ω2、ω3的位置精確平移控制：
把頻率向量H分為兩單邊帶部分H=Hl+H2，其中H1=[l 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0]T,H2=[0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1]T。根據H1、H2，同樣按全相位濾波器構造步驟可分別形成兩個子濾波器h1，h2，根據式(1)和式(5)，其各自對應的濾波器系數分別為(M=3，N=16)：

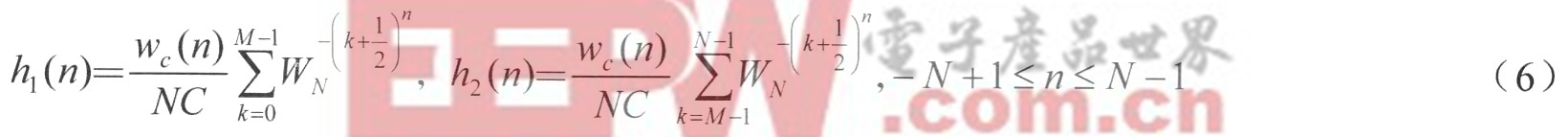
顯然滿足h1(n)=h2*2(n)，從而根據傅立葉變換的性質，有：

如圖3所示：兩者幅頻曲線關于ω=π對稱。

實際要求的截止頻率往往不會恰好落在圖2所示的頻率采樣點上，傳統方法只有增大濾波器長度N來實現來調整邊界頻率。為實現不改變Ⅳ來控制邊界頻率，可把這兩子濾波器曲線進行平移來實現。由于圖3兩子濾波器曲線是對稱的，若將這兩條曲線各自朝相反方向平移相同距離，再把兩子濾波器合成一個濾波器，就可得到實系數的低通濾波器，假設要平移λ個△ω，則平移后的兩子濾波器的FIR系數為：

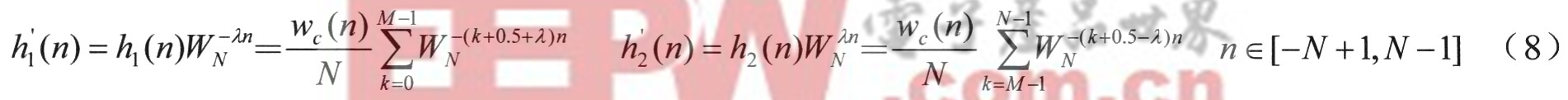
把兩子濾波器系數相加后得到的濾波器系數g’為：

取λ=0．25時，平移后的兩個子濾波器及其復合疊加后的傳輸曲線如圖4(a)、4(b)所示。