基于全相位幅頻特性補償的FIR濾波器設計
控制邊界頻率一直是FIR濾波器設計的難題。傳統的濾波器設計法,如頻率采樣法和窗函數法,因為無法控制臨界頻率,其應用受到限制。而一些現代濾波器設計方法,如神經網絡法…、免疫算法等,這些方法設計的濾波器系數都是借助某種最優化算法對目標幅頻函數進行逼近的過程中得到,但并沒有解決在優化過程中如何控制邊界頻率問題。文獻提出一種FRM(FreqLtency Responses Masking,頻率響應屏蔽)設計法,它首先要設計兩路滿足幅度互補的原型濾波器,再將原型濾波器的每個延時器用M個延時器來代替(即內插過程),然后分別設計兩路屏蔽濾波器去濾除由于內插而產生的鏡像頻率特性,最后將兩路響應疊加即得最后濾波輸出。這樣產生的濾波器系數具有稀疏特性,而總的濾波器長度并不會明顯增加,此方法因為可將過渡帶限制在很窄的寬度內而得到廣泛應用,但該方法存在原型濾波器與屏蔽濾波器的階數、各頻帶波紋相互影響及性能匹配的問題,這些問題通常要用線性規化等復雜數學途徑去解決。
本文在文獻提出的全相位濾波器設計的基礎上,通過變傳統頻率采樣模式為偶對稱的頻率采樣模式,并引入雙相移組合和構造用于補償的全相位單窗濾波器的方法,借助于MATLAB設計,使得FIR濾波器的臨界頻率的位置可通過改變參數λ得以解決,它具有無需多步迭代優化、設計方法簡單的特點。
2 偶對稱頻率采樣下的全相位FIR濾波器
2.1 全相位等效FIR濾波器的設計步驟
文獻提出全相位DFT濾波器設計法,具有頻率采樣法和窗函數法的雙重性質,并指出:濾波器性能可通過加前窗f或后窗b而得以改善,f和b的設定可分為三種情況:無窗、單窗和雙窗。要設計N階全相位濾波器,需先設置一頻率向量H,最終全相位濾波器可等效為長度為2N-1的FIR濾波器,其設計可分為三個步驟:(1)對H進行IDFT生成h,再對h進行定義域延伸,形成(2N一1)長度的向量h’=[h(-N+1)…h(0)…h(N-1)]T。(2)將前窗f、后窗b進行卷積并歸一化后生成卷積窗wc。(3)將h’、wc對應元素相乘即得等效FIR濾波器。根據以上步驟,將生成的2N-l長度的FIR濾波器g的系數推導如下:
設定頻率向量為H=[H(O)H(1)…H(N一1)]T,假設滿足傳統對稱H(k)=H(N-k),(k=1,…,N-1),令H對應的IDFT為k=[h(0)h(1)…h(N-1)]T。令WN=e-j2π/N,對h(n)的定義域進行延拓可得向量h’:

2.2 偶對稱頻率采樣下的全相位FIR濾波器
事實上,H也可設為偶對稱形式,即滿足H(k)=H(N-1一k),(k=0,…,N-1)。如N=16時,可設為:H=[1 1 1 0 0 0 0 0 0 0 0 0 0 1 1 1]T,這時式(1)的IDFT結果為復數,從而式(4)的FIR系數也為復數。為得到實FIR系數,需要將式(4)的g乘以一相移向量v0=[v0(-N+1)…v0(一1)v0(0)v0(1)…v0(N-1)]T,其中![]() 結合式(4),其FIR濾波器系數變為:
結合式(4),其FIR濾波器系數變為:
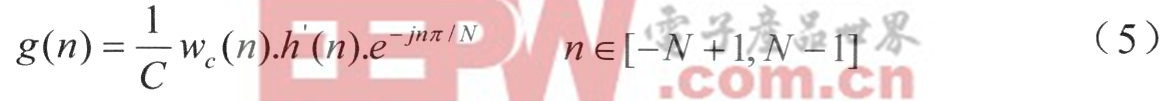
令頻率采樣間隔△ω=2π/N,文獻證明:無窗和單窗全相位濾波器的傳遞曲線嚴格通過頻率設置點k△ω,k=0,1,…,N―l而式(5)對濾波器系數乘以相移向量v0后,根據傅氏變換的頻移性質,其頻率設置點也相應右移0.5△ω,即嚴格通過ω=(k+0.5)△ω,這樣就形成了偶對稱的頻率采樣模式。例:當N=8時,令傳統頻采向量H=[1 1 l 0 0 01 1]T偶對稱頻采向量He=[1 1 0 0 0 0 1 1]T。則這兩種模式在[O,2π)內的采樣點分布如圖1所示。

3 全相位幅頻補償法下的低通濾波器設計
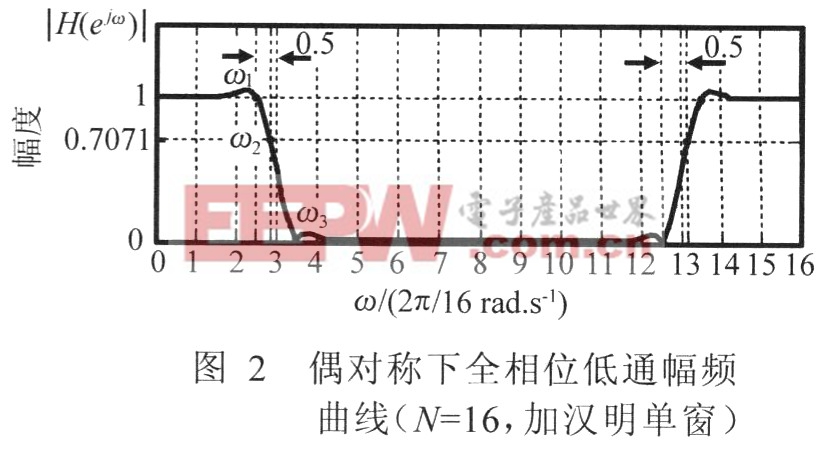
以N=16為例,將偶對稱頻率采樣向量H設為:H=[1 1 1 0 0 0 0 0 0 0 0 0 0 1 1 l]T,在加漢明單窗的情況下,采用前面的全相位FIR濾波器設計步驟,可得到如圖2所示的幅頻曲線。





評論