幾種AM信號數字化解調算法比較
3 基于滑動DFT的AM信號數字化解調算法
以上兩種方法都是對調制信號本身進行處理的,在頻域角度,常用FFT算法對信號進行解調,但這種方法計算量較大,且耗時,這里介紹采用滑動DFT算法對AM信號進行數字化解調。該方法相比于傳統的FFT算法計算量大大降低,具有較高效率。
經A/D采樣后的離散信號表示為:
x(n)=Acos(ωc/fsn+φ), -∞≤n≤+∞
式中:fs為A/D采樣頻率;A,ωc和φ分別對應信號幅度、載波角頻率和初相。
窗口截取信號表示為:

故在解調過程中,僅對載波頻率處所對應的DFT幅度感興趣,取其幅度值去掉直流分量即可恢復原始調制信號。具體運算推導過程如下:
對窗口內的信號在K0=Nfc/fs頻點作DFT變換:
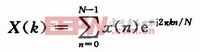
設滑動窗口長度為L,DFT運算點數為N,用X1(K0)表示從第一個采樣數據開始的L個采樣數據進行DFT運算,得到的在頻點K0處的傅里葉值,則有:

這樣即可得到全部采樣數據點在頻點K0處對應的傅里葉值。隨后只需計算|Xn(K0)|,去除直流分量即可恢復調制信號。
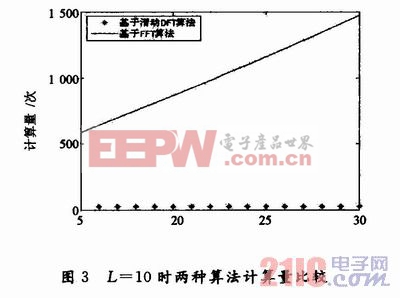
傳統的FFT算法對窗口內的所有時刻都要獨立運算L次,而每個時刻都要Nlog:N次復乘運算口],總計算量為LNlog2N。利用滑動DFT算法,在已知前個時刻頻譜Xn-1(K0)的情況下,計算Xn(K0)只需2次復乘運算,對窗口內的所有時刻總計算量為log2N+2(L-1)。通過圖3的比較可以明顯看出,當N較大時,滑動DFT的計算量遠小于FFT。本文引用地址:http://www.104case.com/article/187313.htm








評論