了解環(huán)形調(diào)制器如何產(chǎn)生AM信號
在調(diào)制器電路中,環(huán)形調(diào)制器是產(chǎn)生AM信號最有效的調(diào)制器之一。在本文中了解原因。
本文引用地址:http://www.104case.com/article/202502/466782.htm調(diào)幅(AM)信號可以使用幾種類型的調(diào)制器電路產(chǎn)生。例如,開關(guān)調(diào)制器將消息信號乘以基頻等于所需載波頻率的周期函數(shù)。這會產(chǎn)生基頻及其諧波的AM波。然后,帶通濾波器將所需的頻譜分量傳遞到輸出端。
我們在前一篇文章中了解了開關(guān)調(diào)制器家族的一個成員,二極管橋調(diào)制器。在本文中,我們將深入研究一種不同的、性能更高的開關(guān)調(diào)制器電路:環(huán)形調(diào)制器。
二極管橋式調(diào)制器綜述
在繼續(xù)之前,讓我們重新審視二極管橋調(diào)制器的關(guān)鍵方面。這將有助于我們更好地理解環(huán)形調(diào)制器的微妙之處,以及它比二極管橋調(diào)制器提供的性能改進(jìn)。
使用二極管橋式調(diào)制器,消息信號(m(t))乘以在零和一之間切換的方波(g(t)。如圖1所示。
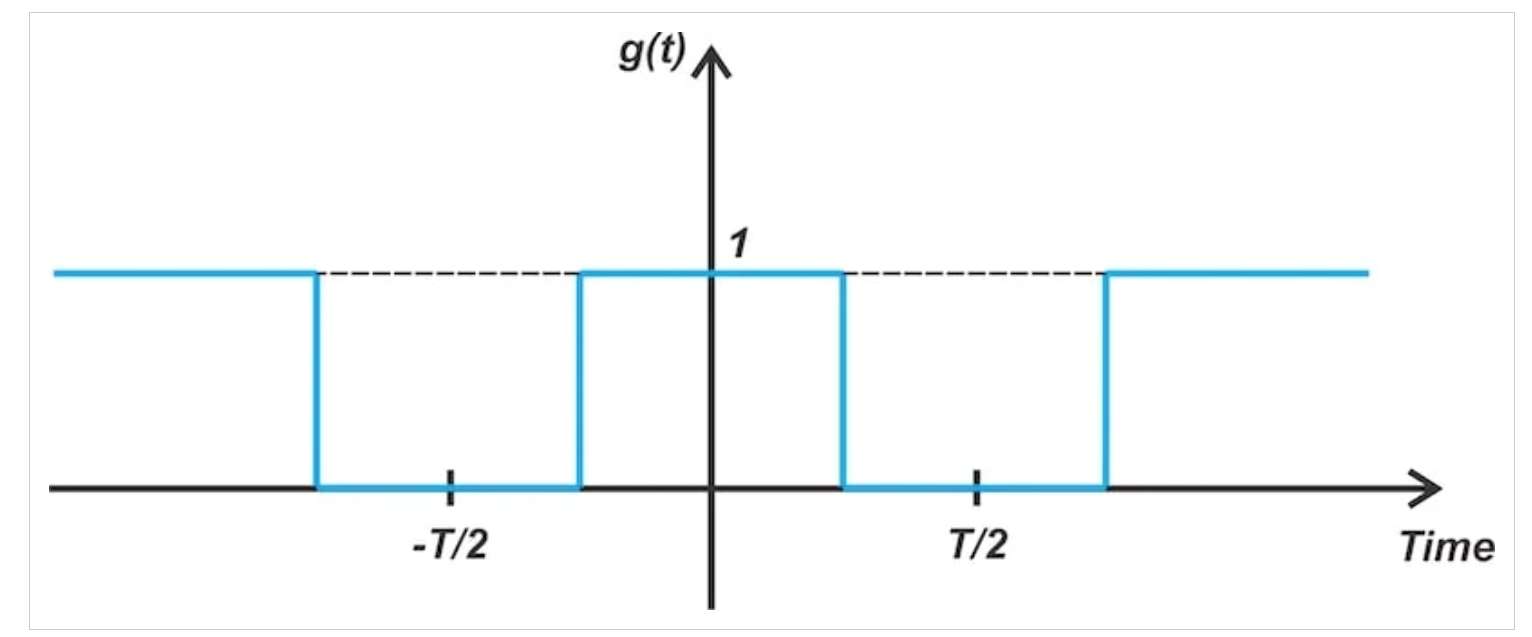
圖1 二極管橋式調(diào)制器中的門控功能
假設(shè)消息信號是單音正弦波,乘以方波會產(chǎn)生圖2中的藍(lán)色波形。
通過帶通濾波器前后的輸出信號。
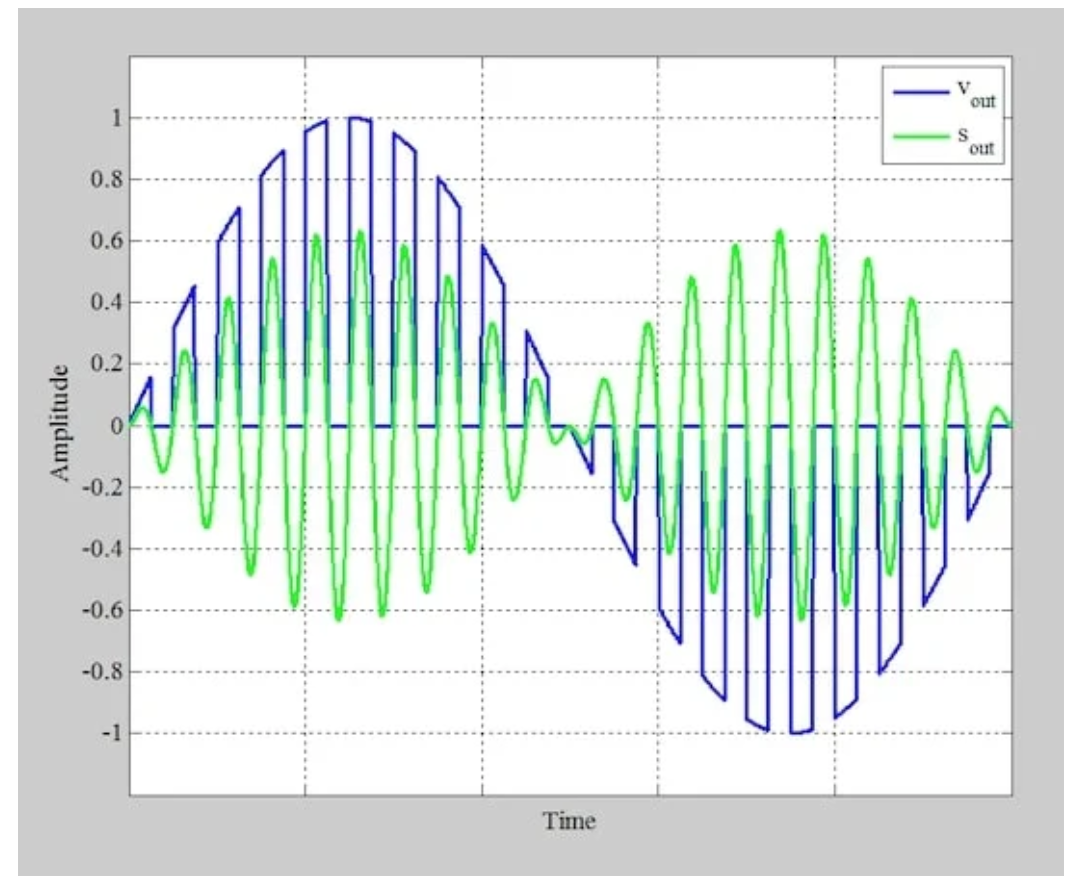
圖2 應(yīng)用門控功能后的信號(藍(lán)色)和帶通濾波器輸出端的結(jié)果信號(綠色)
為了產(chǎn)生最終的AM波,我們需要將藍(lán)色波形通過調(diào)諧到載波頻率(fc)的帶通濾波器。這生成了上圖中的綠色波形。
數(shù)學(xué)分析表明,濾波器輸出端的最終信號由下式給出:
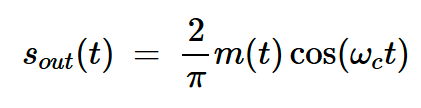
方程式1
在頻域中,乘以圖1所示的方波會產(chǎn)生以0、±fc、±3fc、±5fc等為中心的消息信號頻譜的副本,如圖3所示。
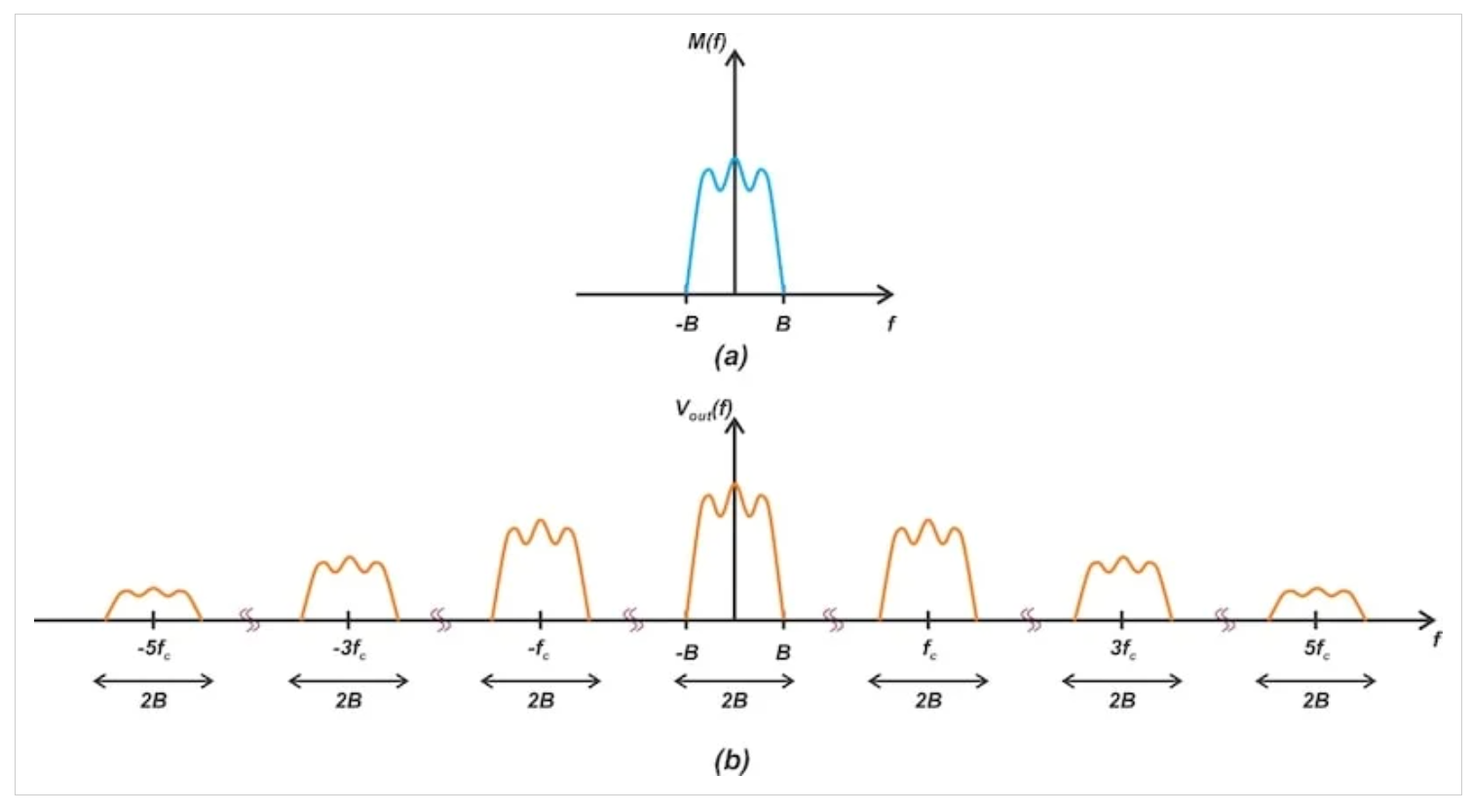
圖3 基帶消息信號(a)的頻譜和在應(yīng)用帶通濾波器(b)之前由調(diào)制器產(chǎn)生的信號
現(xiàn)在我們已經(jīng)回顧了二極管橋式調(diào)制器,讓我們來探索一下環(huán)形調(diào)制器。
環(huán)形調(diào)制器的操作
圖4顯示了環(huán)形調(diào)制器的電路示意圖。它使用四個二極管,它們以形成一個回路的方式排列——這種配置就是以“環(huán)”命名的。
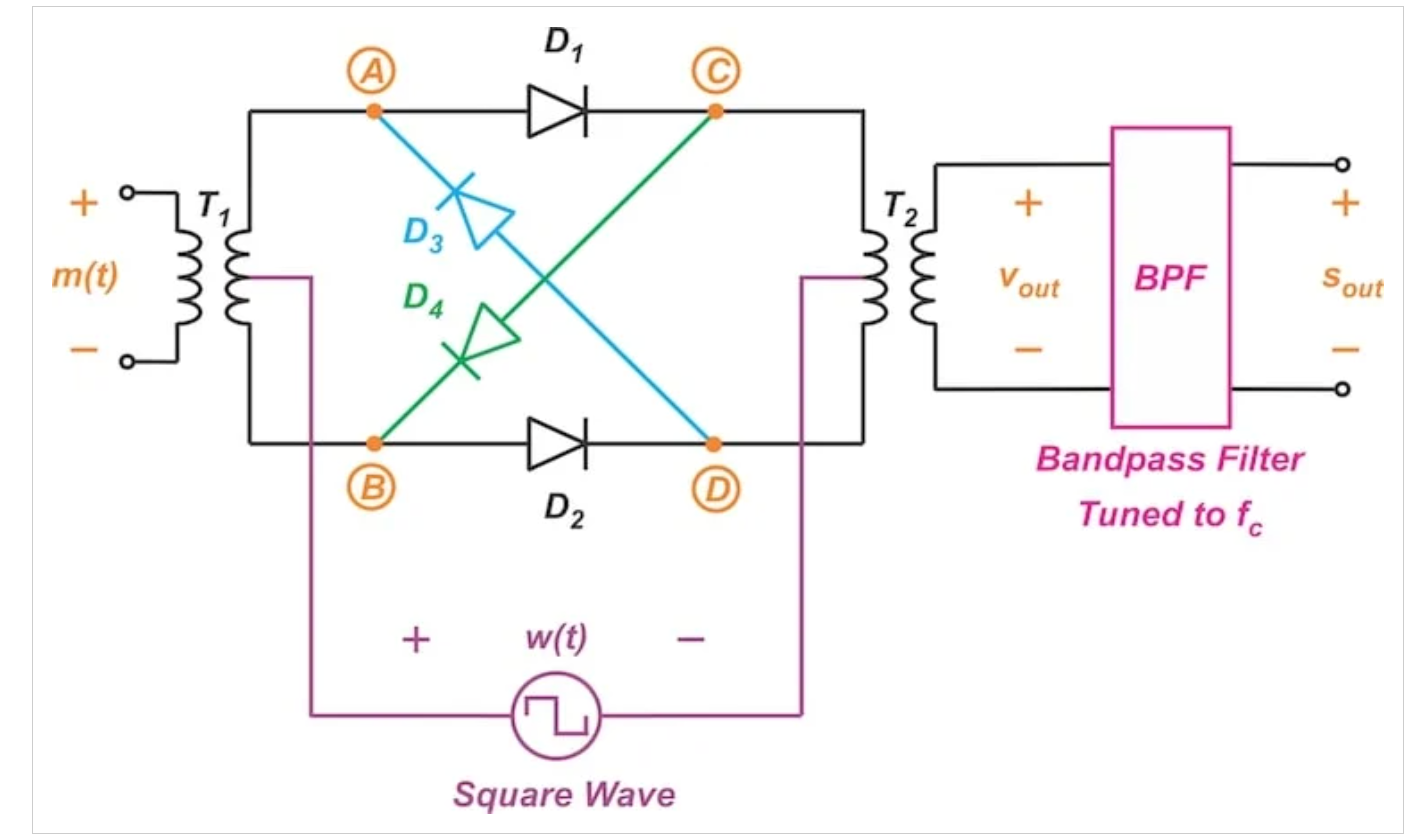
圖4 環(huán)形調(diào)制器示意圖
在圖4的底部,我們看到一個方波(w(t))。該方波的振幅為±A1,被饋入變壓器(T1和T2)的中心抽頭,并以基頻(fc)切換。
當(dāng)w(t)為大正值時,以下情況成立:
二極管D1和D2接通。
橫臂部分(D3和D4)中的二極管關(guān)閉。
節(jié)點A連接到節(jié)點C。
節(jié)點B連接到節(jié)點D。
換句話說,在w(t)的正半周期內(nèi),T1次級兩端的電壓以其原始極性傳輸?shù)絋2初級。
當(dāng)w(t)為大負(fù)值時:
二極管D3和D4接通。
二極管D1和D2斷開。
節(jié)點A連接到節(jié)點D。
節(jié)點B連接到節(jié)點C。
因此,在負(fù)半周期內(nèi),T1次級兩端的電壓以相反的極性傳輸?shù)絋2初級。
實際上,環(huán)形調(diào)制器充當(dāng)換向器,周期性地反轉(zhuǎn)電壓方向。從數(shù)學(xué)上講,消息信號乘以在±1之間切換的方波。如圖5所示。
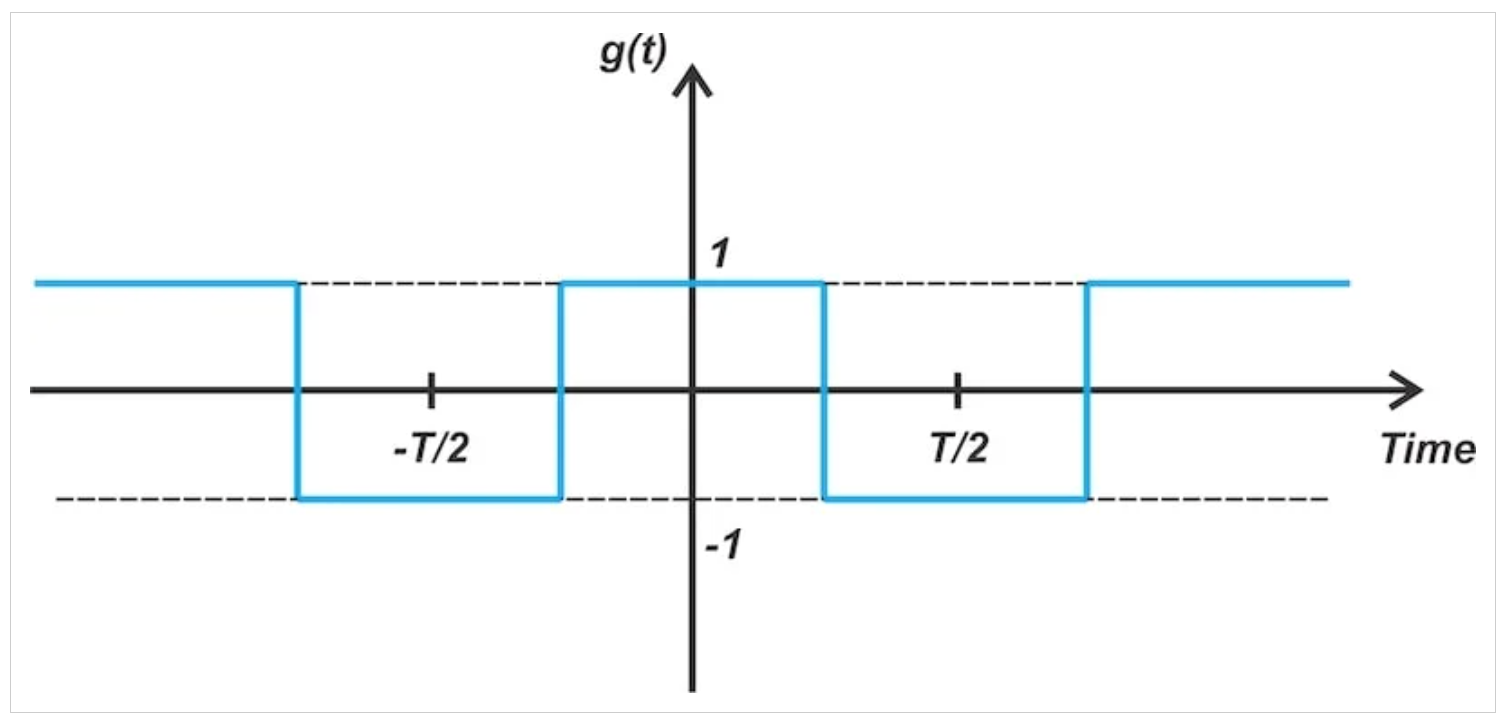
圖5 環(huán)形調(diào)制器中使用的門控功能
接下來,讓我們考慮這個電路的時域波形。
時域波形
與二極管橋調(diào)制器一樣,我們通過向電路施加單音正弦消息信號來檢查時域行為。圖6的上圖顯示了消息信號;下圖顯示了由于電路操作而乘以m(t)的波形。
施加到環(huán)形調(diào)制器的單音輸入(頂部)和有效倍增消息的波形(底部)。
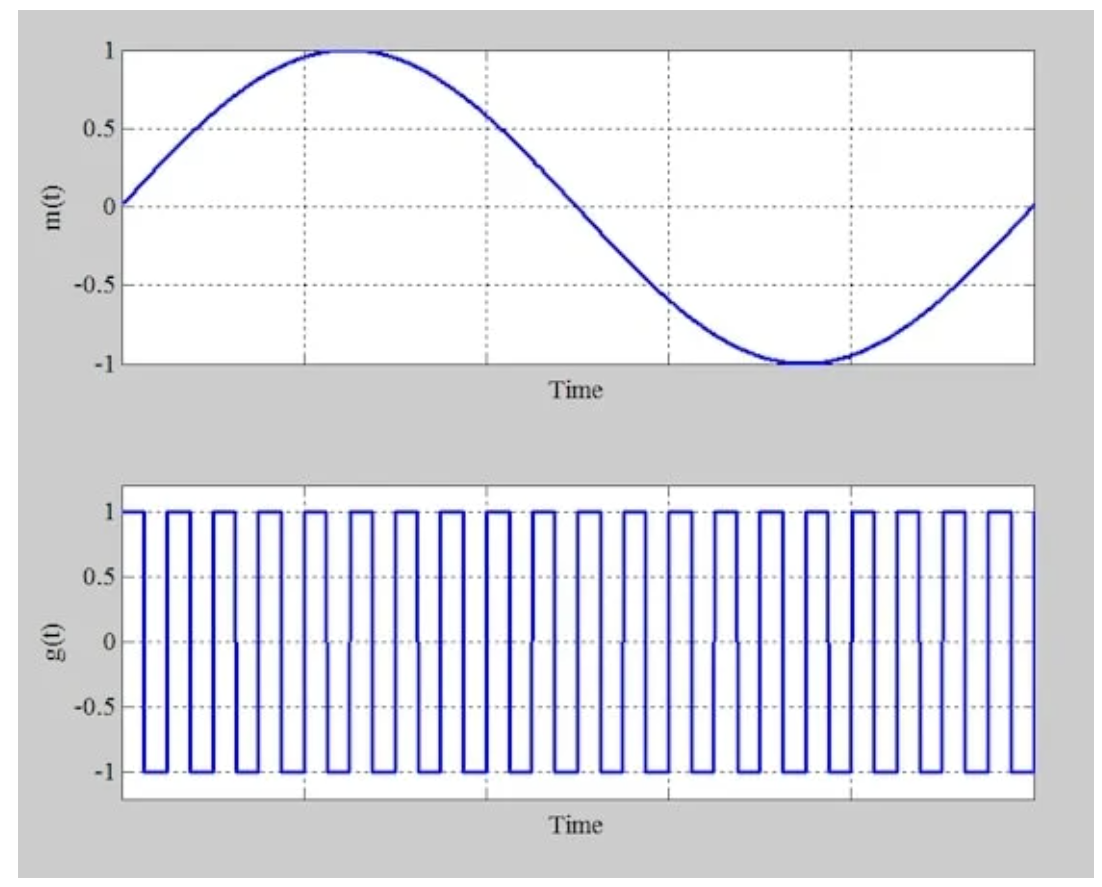
圖6 施加到環(huán)形調(diào)制器的單音輸入(頂部)和有效倍增消息的波形(底部)
我們假設(shè)兩個變壓器的匝數(shù)比為1,所有二極管的電壓降為零。
圖7顯示了將這些波形相乘得到的輸出電壓(vout)。
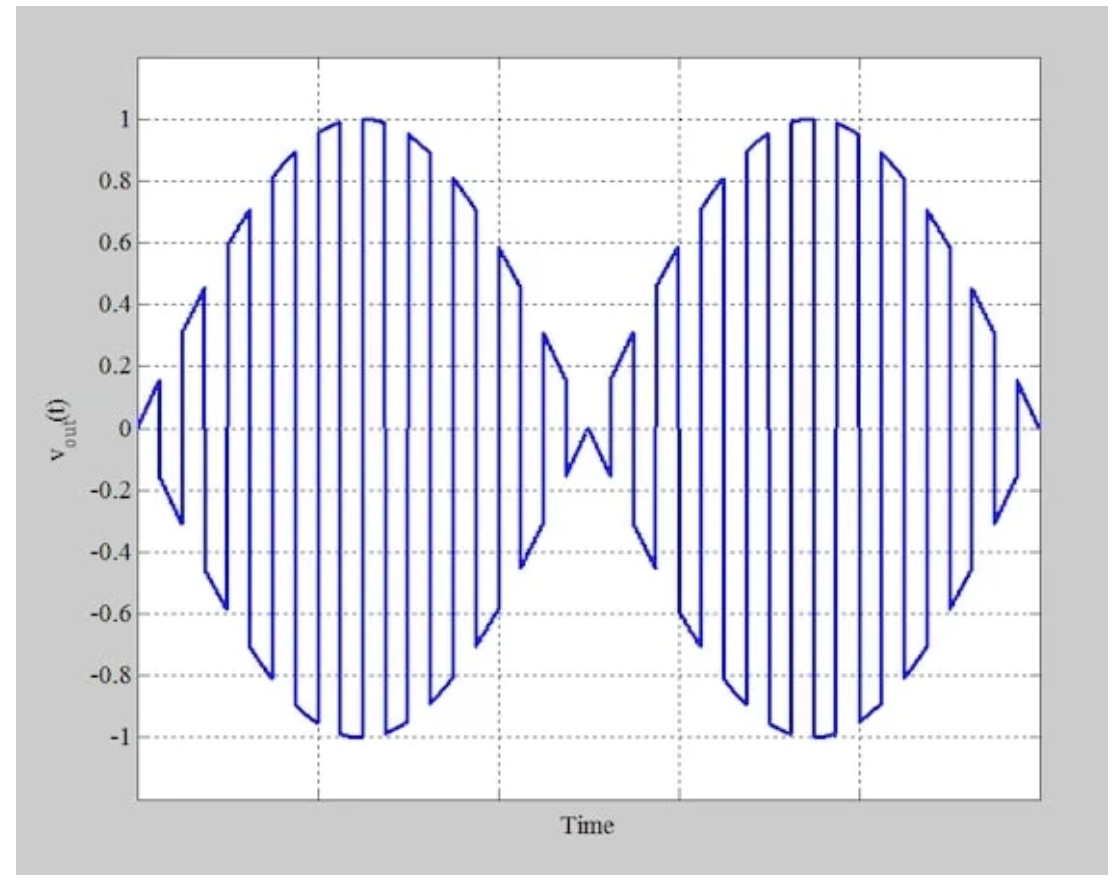
圖7 環(huán)形調(diào)制器產(chǎn)生的輸出波形(vout)
與二極管橋式調(diào)制器一樣,環(huán)形調(diào)制器要求我們通過帶通濾波器來產(chǎn)生最終的AM波。應(yīng)用適當(dāng)?shù)膸V波器會產(chǎn)生圖8中的綠色波形。
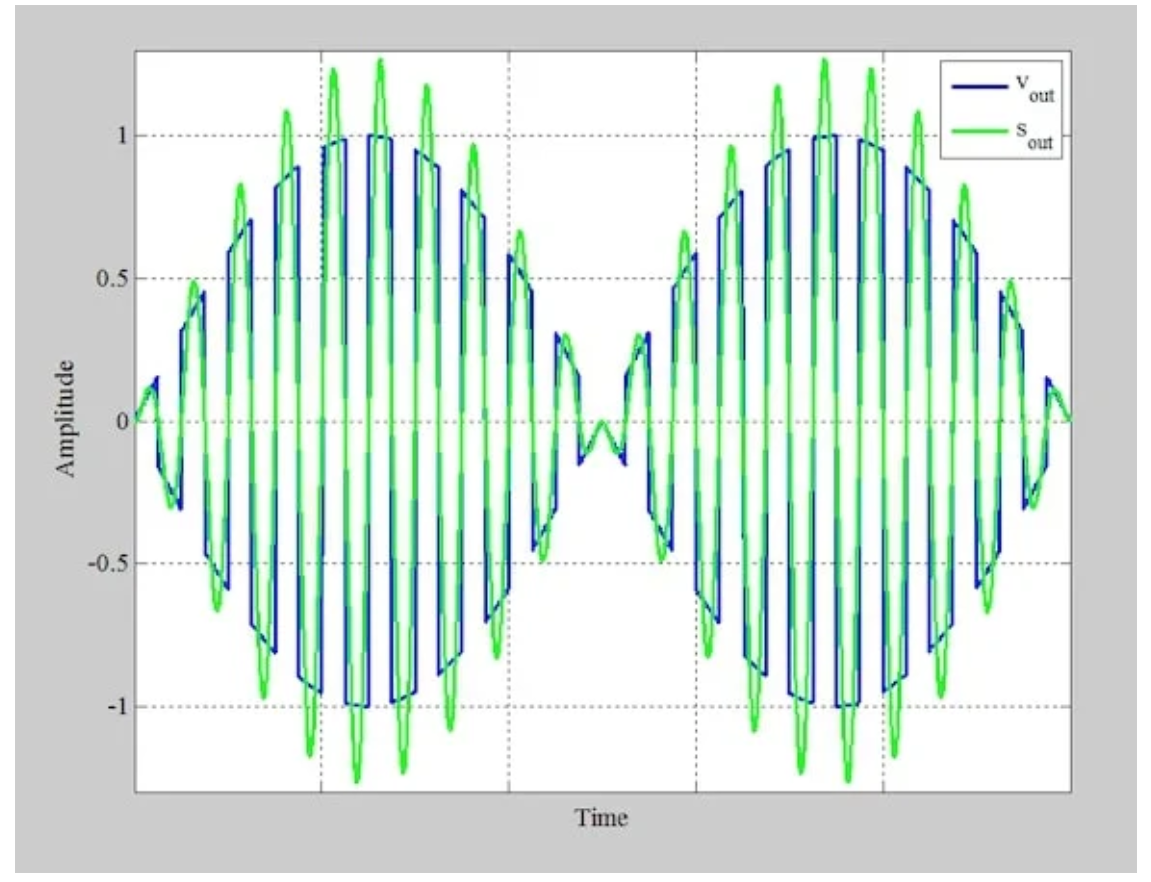
圖8 應(yīng)用門控功能后的信號(藍(lán)色)和帶通濾波器輸出端的最終信號(綠色)
推導(dǎo)輸出信號方程
為了推導(dǎo)輸出信號的方程,我們注意到圖5(g(t))中描繪的門控函數(shù)可以用以下傅里葉級數(shù)展開式表示:
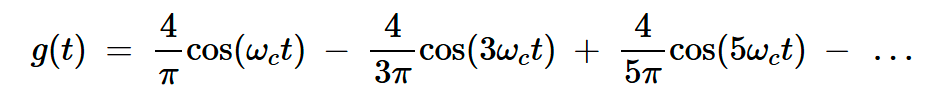
方程式2
注意,由于g(t)是偶數(shù)函數(shù),因此它只能用余弦函數(shù)展開。輸出電壓為:
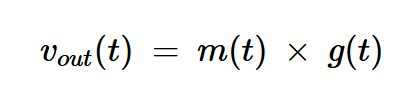
方程式3
結(jié)合上述方程式得出:
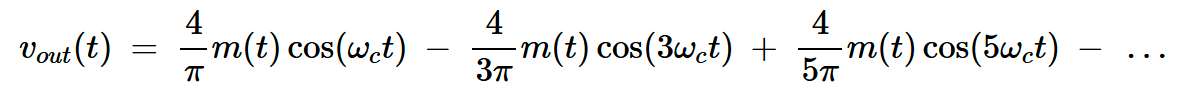
方程式4
方程4表明,vout(t)是以c、±3 c、±5 c等為中心的AM波的疊加。如圖9所示。
基帶消息信號(a)的頻譜和在應(yīng)用帶通濾波器(b)之前由環(huán)形調(diào)制器產(chǎn)生的信號。
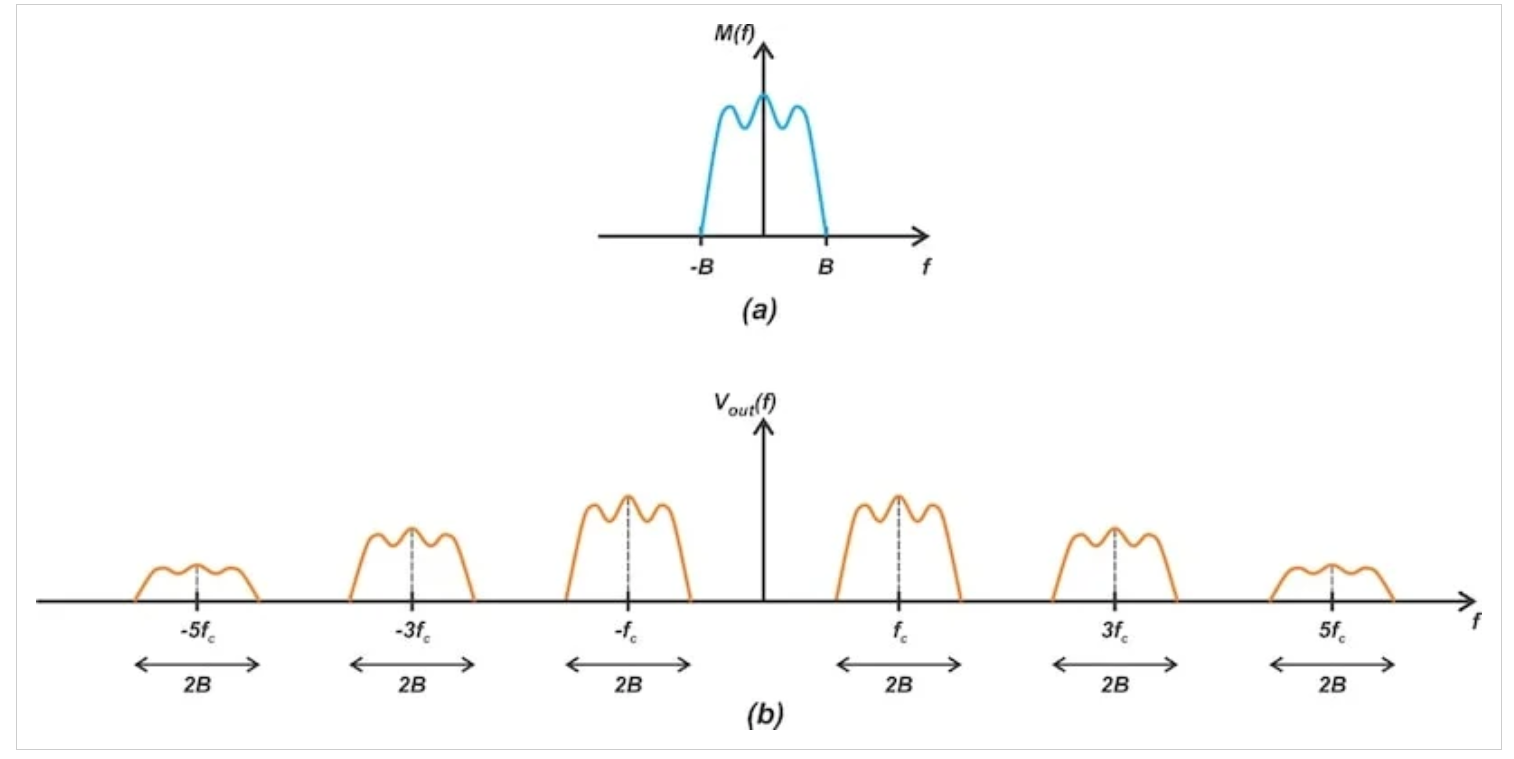
圖9 基帶消息信號(a)的頻譜和在應(yīng)用帶通濾波器(b)之前由環(huán)形調(diào)制器產(chǎn)生的信號
該電路抑制載波,同時保留實際傳輸信息的邊帶。正如我們將在文章的最后談到的那樣,在使用環(huán)形調(diào)制器時也可以保留載波。然而,這在很大程度上超出了本次討論的范圍。
回到圖9,所需的頻譜以fc為中心。為了將其與其他頻譜成分分開,我們應(yīng)該:
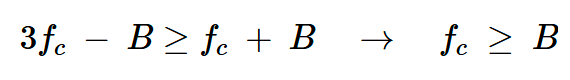
方程式5
這種情況在實踐中很容易實現(xiàn),因為載波頻率與基帶信號帶寬的比率(fc/B)通常在100到300之間。
為了選擇±fc附近的所需邊帶,環(huán)形調(diào)制器包括一個帶通濾波器。使用理想的帶通濾波器,只有以fc為中心的頻譜分量才能通過輸出,導(dǎo)致:
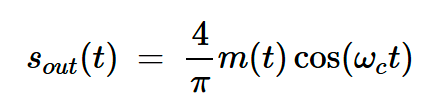
方程式6
二極管電橋與環(huán)形調(diào)制器的比較
現(xiàn)在我們已經(jīng)研究了環(huán)形調(diào)制器的電路、波形和方程,讓我們討論一下它與二極管橋調(diào)制器之間的一些重要區(qū)別。
門控功能的直流分量
二極管橋調(diào)制器的門控功能的直流值為0.5。如圖3所示,將消息信號乘以此門控函數(shù)會創(chuàng)建零頻率附近m(t)頻譜的副本。為了抑制這種頻譜分量,二極管橋調(diào)制器的濾波器應(yīng)該具有(fc-B)-B≈fc的過渡帶。
另一方面,環(huán)形調(diào)制器的門控功能沒有直流分量。因此,我們在圖9中看到,在輸出端的零頻率附近沒有出現(xiàn)頻譜分量。相反,最接近的光譜分量集中在3fc處。
這會影響帶通濾波器過渡帶的銳度。為了抑制以3fc為中心的頻譜分量,環(huán)形調(diào)制器需要一個過渡帶為|(fc+B)?(3fc-B)|≈2fc的濾波器。
時域波形的對稱性
要了解環(huán)形調(diào)制器如何消除以f=0為中心的頻譜分量,請考慮其時域波形。檢查這些波形,我們看到環(huán)形調(diào)制器在濾波器輸入端產(chǎn)生的信號關(guān)于零對稱。這種對稱性消除了零頻率(DC)下的消息信號頻譜。
這種對稱性之所以出現(xiàn),是因為環(huán)形調(diào)制器在交替的半周期內(nèi)輸出具有原始或反轉(zhuǎn)極性的消息信號。相比之下,二極管橋調(diào)制器產(chǎn)生的信號在半個周期內(nèi)等于消息信號,在另一個周期內(nèi)降至零。
雙平衡與單平衡
在帶通濾波器的輸入端,環(huán)形調(diào)制器僅產(chǎn)生乘積項。它抑制了消息和載波信號。因為它抵消了基帶信號和載波,所以我們稱環(huán)形調(diào)制器為雙平衡。
另一方面,二極管橋調(diào)制器僅相對于載波輸入保持平衡。消息信號出現(xiàn)在帶通濾波器的輸入端,使其成為一個單平衡調(diào)制器。
輸出電壓電平
比較方程1和6,我們觀察到環(huán)形調(diào)制器產(chǎn)生的輸出電壓是二極管橋式調(diào)制器的兩倍。這與圖2和圖8所示的綠色波形一致。這些圖分別顯示了最大振幅為0.63和1.26的AM波。
總結(jié)
環(huán)形調(diào)制器在一個半周期內(nèi)以原始極性將輸入信號傳輸?shù)捷敵龆耍诮惶娴陌胫芷趦?nèi)則以相反的極性傳輸。這放寬了帶通濾波器的過渡帶要求,并使輸出信號的幅度加倍。應(yīng)該指出的是,防止載波功率泄漏到環(huán)形調(diào)制器的輸出中需要完全平衡的變壓器和匹配的二極管。
另外,環(huán)形調(diào)制器還可以用于產(chǎn)生不抑制載波的AM信號。為了理解如何,我們注意到環(huán)形調(diào)制器有效地充當(dāng)了乘法器。由于對輸入消息信號沒有限制,我們可以通過向環(huán)形調(diào)制器施加具有任意調(diào)制指數(shù)的1+μm(t)來產(chǎn)生傳統(tǒng)的AM信號。



評論