MOSFET管并聯應用時電流分配不均問題探究
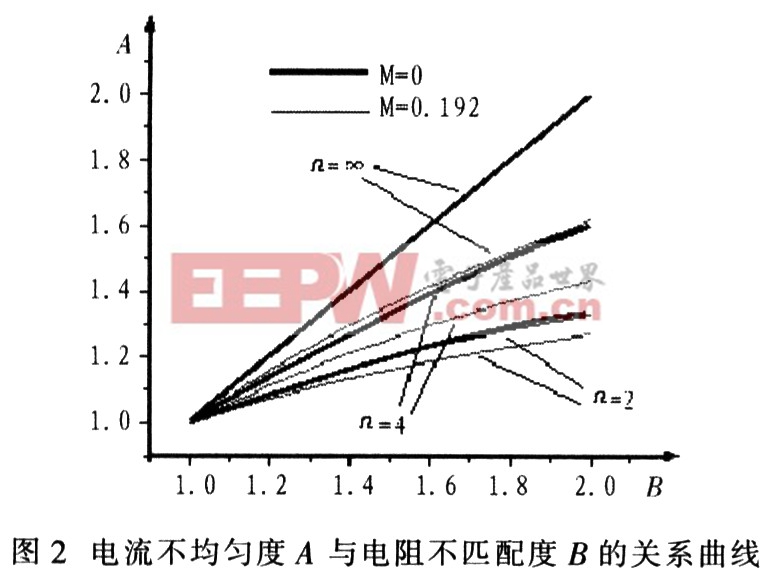
圖2是以IRFP064為例,根據式(6)~(9)計算出的漏極電流不均勻度A與導通電阻均勻度B間的關系曲線(以n為參變量),可得出如下結論:(1) 并聯器件數n相同的每一組曲線,漏極電流不均勻度A隨自主補償系數M的增大而下降;(2)并聯器件數n相同的每一組曲線,兩條曲線間的差距隨n的增大而增大;(3)并聯器件數n相同的每組曲線,隨n的減小而降低;(4)并聯器件的靜態電流不匹配度A有最大值,即A=B。所以,降低并聯器件的電流不匹配度的最有效方法就是提高并聯器件導通電阻的匹配程度。本文引用地址:http://www.104case.com/article/181198.htm

3 閾值電壓UT對動態電流分配的影響
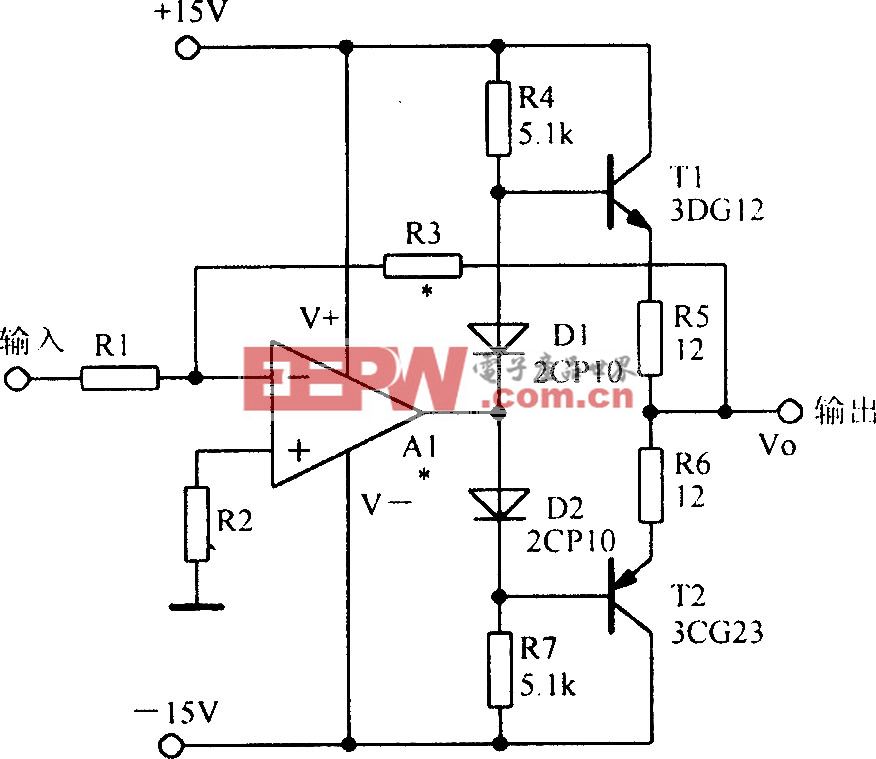
動態電流分配不均是指由于器件本身參數失配而使各并聯支路在開關過程中電流大小不一致的現象。原因很多,這里以圖3為例分析閾值電壓UT引起的電流分配不勻現象。
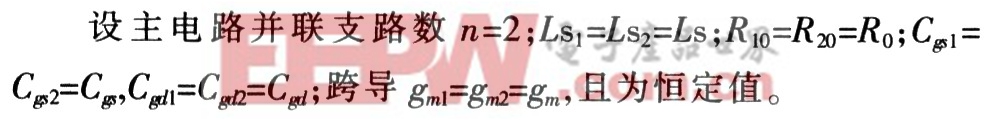
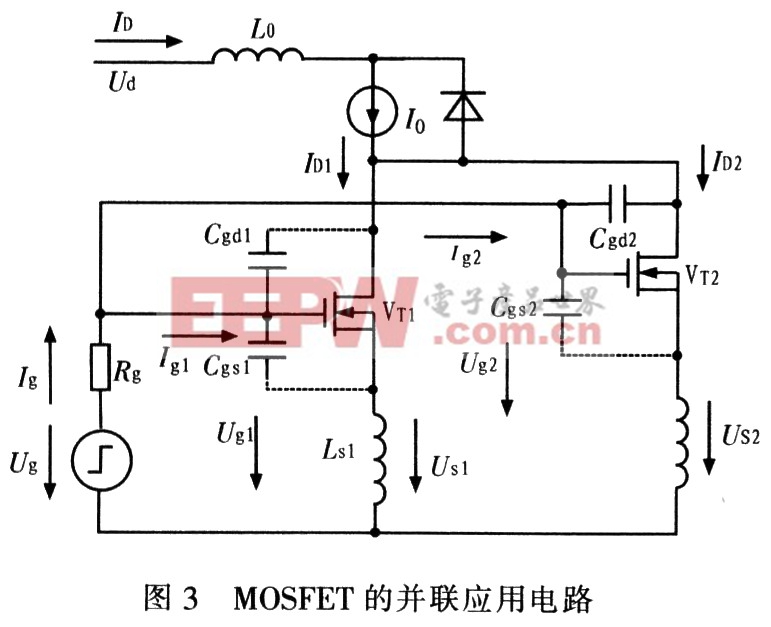
3.1 VT1、VT2均未導通時的柵極電壓,0→t1時段,iD1=iD2=0
柵極驅動信號由負半周進人正半周后,信號源Ug向兩管的柵極電容Cgs充電,即:
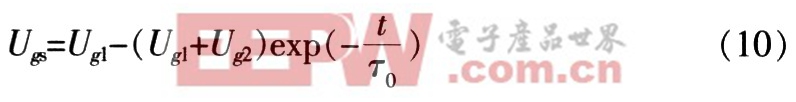
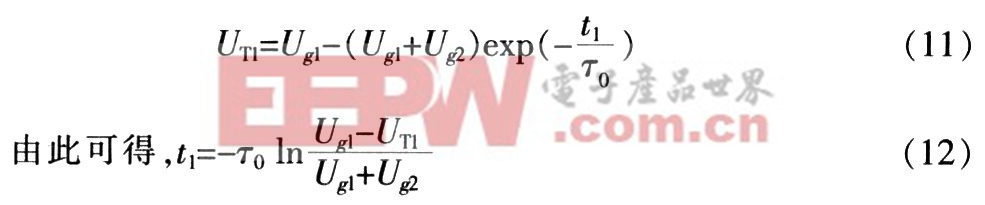
3.2 僅VT1管導通時的柵極電壓,t1~t2時段
在t1~t2時間段內,iD1>0,iD2=0。對其整理,得到二階微分方程組:
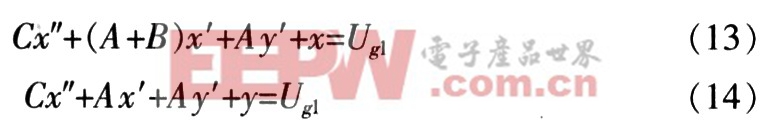
式中,變量系數的數量級為A≈10-8,B≈10-5,C≈-10-13。下面分析中認為B>>A>>C。考慮t1~t2時間段變量x的初始條件,t=0時(即上一階段t=t1時);x=UT1;并選擇x'=0,并考慮微分方程中變量系數的數量級關系,得此微分方程組的解為:

3.3 兩管均導通時的柵極電壓,時段t2~∞
在t2~∞時間段內,iD1>0,iD2>0根據圖3,可整理得出二階微分方程組為:
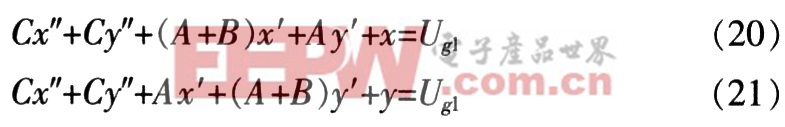
式中,C=2RgCgdgm(L0+LS),同上述略有差異,但這種差異對結果影響甚微,予以忽略。
基爾霍夫電流相關文章:基爾霍夫電流定律












評論