帶Smith預(yù)估器的預(yù)測(cè)PID控制器的設(shè)計(jì)
圖3中,在110s處設(shè)定值發(fā)生幅值為20%、寬度為10s的脈沖擾動(dòng),以及在200s處,對(duì)象模型躍變?yōu)锳1(z-1)=1-0.99z-1+0.25z-2,以及B1(z-1)=0.57+O.31z-1。從圖中結(jié)果的對(duì)比可以看出,預(yù)測(cè)PID(β=0.95)比常規(guī)PID(Z-N法整定)控制器具有更好的動(dòng)態(tài)響應(yīng)特性,并且在出現(xiàn)外部擾動(dòng)以及對(duì)象內(nèi)部特性發(fā)生變化時(shí)體現(xiàn)出了更強(qiáng)的抗干擾性與魯棒性。本文引用地址:http://www.104case.com/article/163514.htm
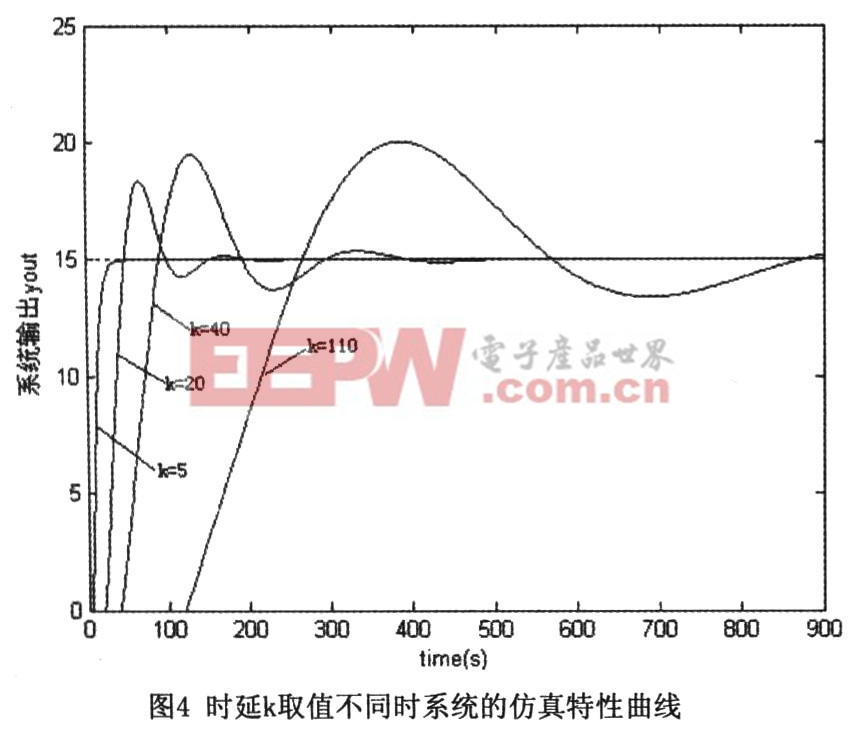
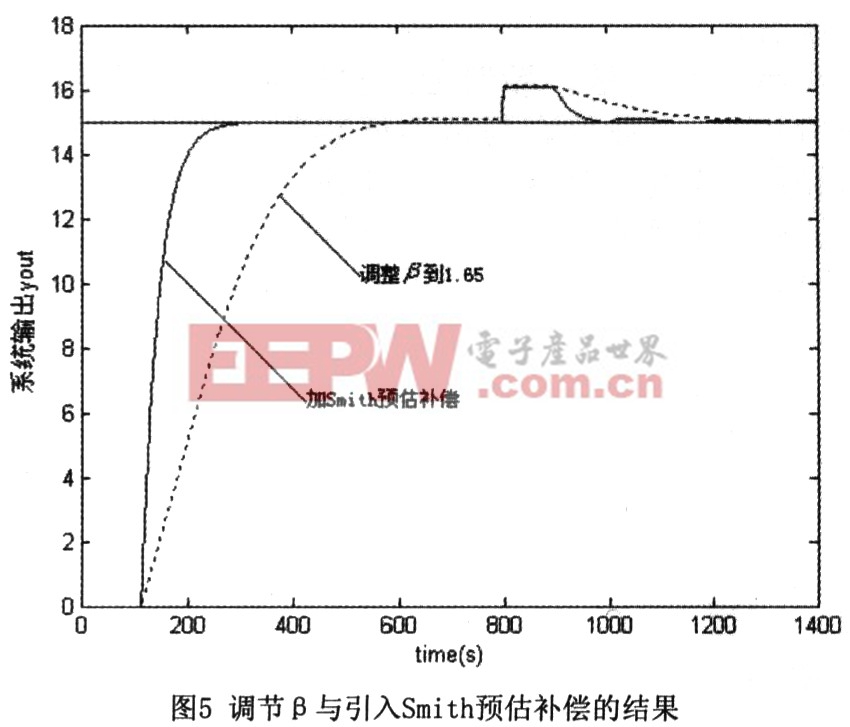
圖4則是在其他參數(shù)保持不變(β=1.35),時(shí)延步數(shù)分別取值為5、20、40與110時(shí),系統(tǒng)(無(wú)Smith補(bǔ)償)的響應(yīng)特性曲線,可以發(fā)現(xiàn),隨著時(shí)延的增加,系統(tǒng)的超調(diào)量及響應(yīng)時(shí)間都有所增加,動(dòng)態(tài)性能逐漸變差。由前文的分析可知,系統(tǒng)的動(dòng)態(tài)響應(yīng)性能可以通過改變?chǔ)碌拇笮?lái)調(diào)節(jié),另外在大時(shí)延系統(tǒng)中也可以通過引入Smith預(yù)估器來(lái)補(bǔ)償時(shí)延,這里以k=110為例,對(duì)這兩種方法進(jìn)行比較,結(jié)果如圖5所示(800s處模型躍變?yōu)锳1(z-1),B1(z-1)以及時(shí)延k變?yōu)?00)。很顯然,增加B的值,雖然可以很好地改善系統(tǒng)的超調(diào)量,但卻無(wú)法兼顧系統(tǒng)的響應(yīng)時(shí)間,這對(duì)于那些對(duì)系統(tǒng)超調(diào)及響應(yīng)時(shí)間都有要求的對(duì)象來(lái)說(shuō)是不可取的,而加入Smith預(yù)估補(bǔ)償?shù)姆椒ǎ瑒t可以消除延時(shí)的影響,使大時(shí)延系統(tǒng)的超調(diào)量及響應(yīng)速度都得到大大改善,并且很好地保持了系統(tǒng)的魯棒性。
4 結(jié)論
文中討論了基于SGPC的PID參數(shù)整定問題。仿真結(jié)果表明,此方法較常規(guī)PID具有更好的控制性能,而且自適應(yīng)Smith預(yù)估器的引入可以克服大時(shí)延系統(tǒng)的整定誤差,并且充分保持了系統(tǒng)的魯棒性。本研究為工業(yè)過程控制中的大滯后、時(shí)變等復(fù)雜系統(tǒng)的控制提供了一種良好的選用方案。
pid控制器相關(guān)文章:pid控制器原理









評(píng)論