帶Smith預估器的預測PID控制器的設計
0 引言
PID控制器因算法簡單、魯棒性好、可靠性高,一直是工業生產過程中應用最廣的控制器。然而,實際生產過程往往具有非線性、時變不確定性,應用常規PID控制不能達到理想的控制效果。這時,往往不得不采用模型預測控制、自適應控制等先進控制策略來獲得更好的控制性能。但是也存在多種原因阻礙這些先進控制策略在實際中的應用。其中一個主要的原因就是由于這類先進的控制算法在硬件、軟件和人員培訓方面缺乏有效的支持,這阻礙了它們在DCS層上的實現。而且在參數整定方面,由于這類算法的參數常缺乏明確的物理意義,對于已熟悉PID參數整定的操作人員來說,也是不得不面對的問題。因此,近年來越來越多的研究人員就上層采用模型預測控制這類先進的控制算法,而底層保留傳統的PID控制算法,即所謂的預測PID控制算法,展開了一系列的研究。如P.Vega等人直接將經典PID的參數引入到性能指標中,再通過Taylor近似處理得到了次優化的控制器參數。Miller提出了一種隨機預測PID控制算法,其在數學上等于穩態加權廣義預測控制算法,并先后成功應于化肥廠熱交換器的溫度控制和廢水裝置溶氧濃度的控制。在文獻[5]中,MASARU KATAYAMA根據PID與一般GPC控制律之間的對應關系,直接計算出PID參數的值,本文在其基礎上,采用階梯式策略,避免了參數整定過程中復雜的矩陣求逆運算,并給控制輸出引入較強的階梯約束,改善了控制性能的調節靈活性。另外,文中分析了該方法在整定大延時對象的控制器參數時所引起的誤差的原因,并通過引入smith預估器,有效地改善了這類系統的控制效果。
1 整定算法
1.1 系統描述及PID控制律介紹
考慮到GPC算法的需要,本文采用受控自回歸積分滑動平均模型(CARIMA)描述被控對象:![]()
其中,y(t)和u(t)為系統在t時刻的輸出值和控制量;ζ(t)為零均值、方差有界的白噪聲;k為系統的最小時延;△=1-z-1為差分算子;A(z-1)、B(z-1)分別為后移算子z-1的na和nb階多項式,且A(z-1)為首一多項式。
文中控制器采用I-PD型結構,該控制律在改變設定值時,控制器輸出不至于有太大的變化,增強了系統的抗擾動能力,另外可以很方便地得到此I-PD控制律與GPC控制律之間的聯系,從而可以依據GPC思想來進行PID參數的整定。其具體形式為: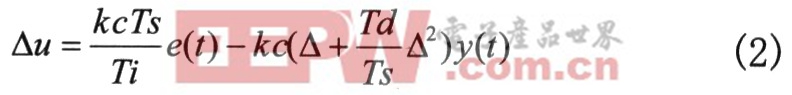
其中,e(t)=w(t)-y(t)為誤差信號,w(t)為參考信號,kc、Ti、Td分別為比例增益、積分時問和微分時間,Ts為采樣時間。對上式進行展開整理可得如下形式:

1.2 SGPC算法
按照GPC的一般理論,由模型(1)和Diophantine方程,得到t時刻對未來t+k+i(i=0,1,L,P-1)時刻系統輸出的最優預測:
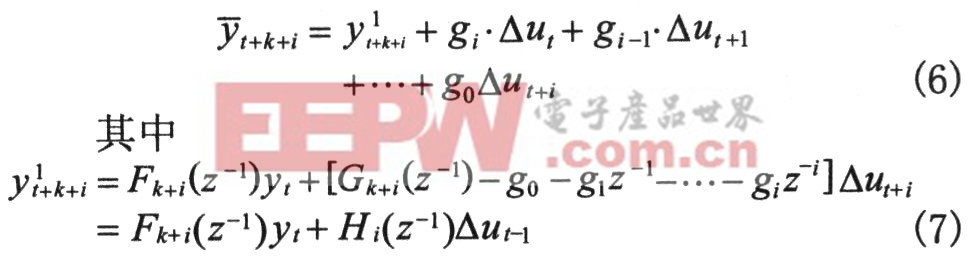
為最優預測中的自由響應部分,Fk+i(z-1)和Gk+i(z-1)是由Diophantine方程確定的z-1的多項式,![]() 是對象階躍響應的第l項系數,可以寫成矩陣形式Y=Y1+G?△U,則實際的輸出為Y=Y+E,E為誤差向量。
是對象階躍響應的第l項系數,可以寫成矩陣形式Y=Y1+G?△U,則實際的輸出為Y=Y+E,E為誤差向量。
GPC一般性能指標為
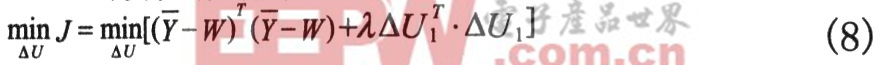
其中△U1=(△ut△ut+1…△ut+m-1),m為控制步長,λ為控制增量的權重。
pid控制器相關文章:pid控制器原理









評論