帶Smith預估器的預測PID控制器的設計

由Diophantine方程可知F(1)=Q，因此式(13)亦可表示為式(5)的形式，此時

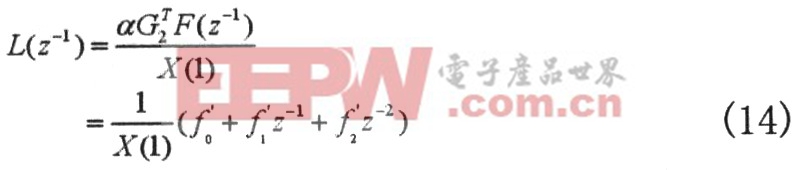
1.3 整定結果

由式（4）與式（14）的對應關系，我們可以比較得到PID控制器各參數（其中Ts為采樣周期）如下：

2 整定算法的分析

2.1 參數調節的問題

本文通過引入階梯因子，避免了參數整定過程中矩陣求逆，大大簡化了計算。同時，在實際系統中，由于執行機構性能的限制，若控制量變化頻率高，不僅執行機構動作跟不上，起不到作用，而且會增加執行機構的磨損。而階梯式策略假定控制增量服從一個等比序列，這相當于給控制增量加了一個較強的限制。另外，由于引進階梯因子后，加權因子λ性能的影響減小，而且其對于控制量的抵制作用也變得比較復雜，因此我們主要可以通過β來調節對應PID控制器的魯棒性與快速性。

2.2 整定誤差的Smith補償

在前述的算法推導中，可以發現，為了建立I-PD與SGPC之間的相互聯系，對多項式X（z-1）進行了靜態處理，由式（12）與 式（13）可以看出，這樣的處理，相當于認為過去k+nb-1步的輸入變化量都相等，且等于當前時刻的輸入變化量，即△ut-knb+1=△ut-k-nb+2=…=△ut，而實際運行中，在系統動態響應階段，這種關系顯然總是不成立的。這種近似處理，在系統無延時或小延時，即k取值很小時，影響可以忽略，但隨著時延步數的加大，這種處理對系統魯棒性地影響必將逐漸加劇，所以需要對具有大延時的系統進行補償。因此，本文在系統中引入Smith預估器，以消除系統的時延影響，改善大延時系統的控制效果。

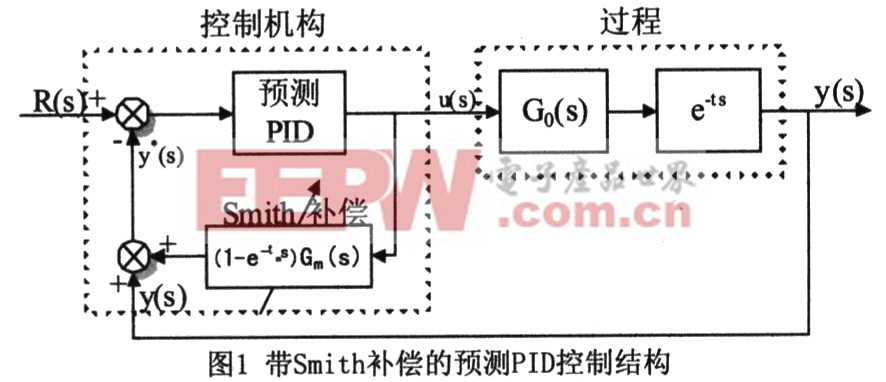
由于常規Smith預估器在模型失配時存在低魯棒性問題，因此在應用中可采用文獻[8]中的自適應方案，即首先通過單變量尋優方法估計實際過程的純滯后，然后再用帶遺忘因子的最小二乘法辨識過程模型的其他參數，以在線修正模型。這樣系統的控制結構可以設計成圖1所示的形式。從圖中可以看出，若系統無延時，系統等同于簡單的預測PID控制回路，而當系統有時延時，延時對系統的影響即可由smith預估器消除，而預測PID參數則僅需根據無時延模型Gm(s)來整定，這樣就可以避免時延帶來的參數整定誤差。

3 仿真及分析
為仿真需要，考慮以下單變量模型：

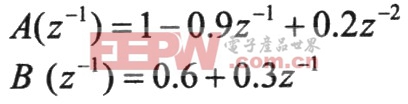
P=10，m=5，λ=1，B與k的值按仿真需要選取。

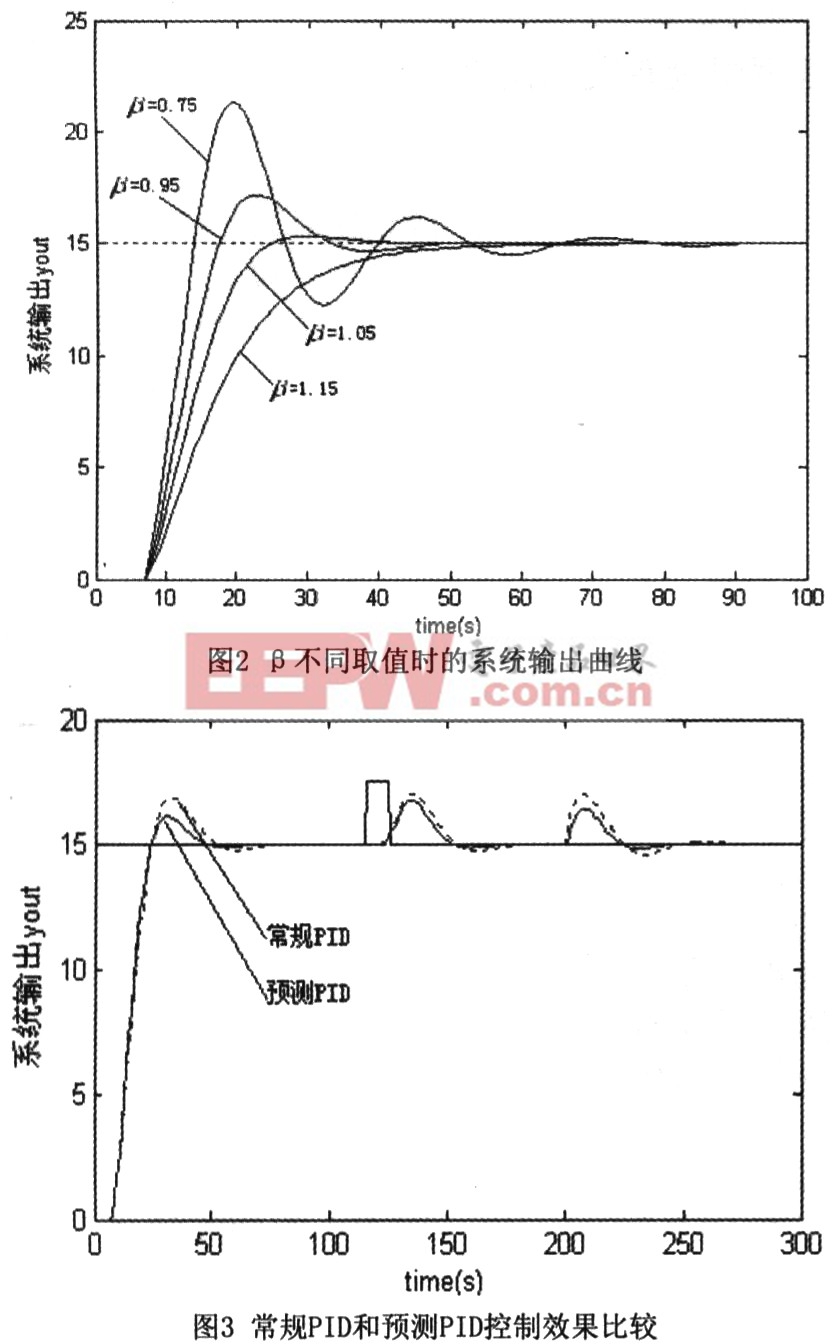
圖2所示為K=7，β分別取0．75、0．95、1．05與1．15時，PID控制系統(無Smith補償)的響應輸出曲線，從圖中可見，基于SGPC整定的PID控制器的動態性能可以很容易地通過選擇不同的B值來調節，以獲取合適的控制器參數，隨著B取值的增加，系統的超調越小，響應速度則越慢，充分保持了SGPC控制的這一特點。