多變量系統(tǒng)辨識及其PID解耦控制的研究
對于圖1中的典型系統(tǒng),當(dāng)系統(tǒng)穩(wěn)定后,斷開u1、u2,給u2加入階躍信號,記錄下y1、y2的值,然后代入式(2)~式(12)辨識出G11(s),G21(s)。同理,u2加入階躍信號,令u1=O,辨識出G12(s),G22(s),從而系統(tǒng)的傳遞函數(shù)矩陣求出

2 滯后環(huán)節(jié)近似
由于得出的模型含有滯后環(huán)節(jié),而滯后環(huán)節(jié)不能夠直接解耦,所以比較各種近似方法,通常近似方法為:一階pade近似、二階對稱pade近似、二階非對稱Pade近似。文獻對其多次進行實驗發(fā)現(xiàn)一階Pade逼近在初始時刻有波動,但在滯后較大的情況下逼近效果較好,這是因為Pade逼近引入零點的原因,二階對稱Pade逼近效果最差,而且二階對稱Pade逼近除了在初始時刻有波動還產(chǎn)生了超調(diào)量。二階非對稱Pade逼近調(diào)節(jié)時間較短,且無明顯的超調(diào)量,但是波動較大。因此采用移位處理和二階泰勒級數(shù)展開即全極點近似法

通過仿真驗證發(fā)現(xiàn)全極點型近似方法由于避免引入零點,所以誤差最小,其要比Pade逼近調(diào)節(jié)時間短,而且沒有超調(diào)量,即能更好的獲得階躍響應(yīng)特性。
3 解耦控制
多輸入多輸出系統(tǒng)內(nèi)部結(jié)構(gòu)復(fù)雜,存在有一定程度的耦合作用,對于這種存在耦合的對象,工業(yè)過程控制要求系統(tǒng)能夠安全穩(wěn)定地運行,又有較好的調(diào)節(jié)性能,能以較小的誤差跟蹤設(shè)定值的變化,并使穩(wěn)態(tài)誤差為零。為了達到高質(zhì)量的控制性能,必須進行解耦設(shè)計。如何把它們間的耦合作用去掉變成獨立的單變量系統(tǒng)進行控制是解決多變量控制的一種重要的方法,去掉耦合的過程就是解耦。其中常用的解耦方法有對角矩陣法、逆Nyquist曲線法和特征曲線法。其中對角矩陣法在過程控制領(lǐng)域中起到很大作用。

式(15)是一個多變量系統(tǒng)傳遞函數(shù)矩陣,對角矩陣解耦就是將耦合對象傳遞函數(shù)矩陣變成一個對角形矩陣的形式即式(16)所示,除主對角線上的元素外,其他元素均為零。這樣輸入U(s)與輸出Y(s)就成為一一對應(yīng)關(guān)系,以達到便于控制的目的。
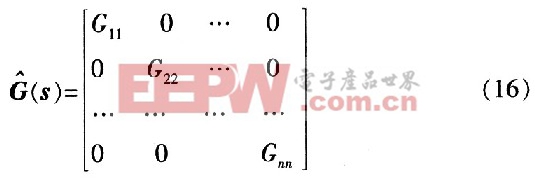
假設(shè)為了使傳遞函數(shù)矩陣轉(zhuǎn)變?yōu)閷顷嚕赨(s)的輸出端加入一個n×n的矩陣D(s)

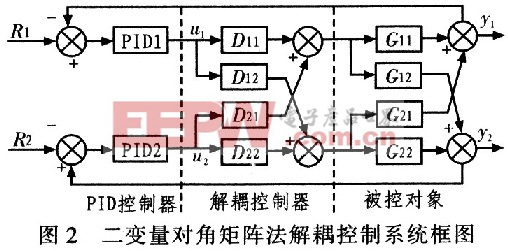
由于采用上文所提的方法辨識出的模型是奇異矩陣的幾率很小,以二輸入二輸出系統(tǒng)為例,假設(shè)G(s)為一個非奇異方陣,則有逆矩陣存在。針對PID控制器的解耦控制系統(tǒng)框圖如圖2所示。本文引用地址:http://www.104case.com/article/162892.htm
pid控制器相關(guān)文章:pid控制器原理






評論