微陣列加速度傳感器的設計理論

建立引信系統環境識別(如多向加速度)與參數估計的多維信息處理理論產生新的引信原理是當前重要的研究方向。如對硬目標的侵徹或貫穿裝甲所使用的巡航導彈、激光制導炸彈等，都存在多向加速度的探測問題。因此大量程的能測量105 g微加速度計具有非常重要的應用價值。目前微陣列式加速度計發展非常
迅速，它對提高武器作戰水平，改進武器性能起著十分重要作用。另外汽車上的安全氣囊，在微機器人中，執行器動作的運動速度、加速度和力的大小的檢測都需要微陣列式加速度傳感器。因此微陣列式加速度傳感器的應用范圍廣，前景十分看好。
隨著集成電路平面加工工藝技術日趨成熟，微加工中的三維加工工藝不斷地發展，使微傳感器、微馬達、微泵等制造已成為現實。文獻[1]曾提出了傳感陣列的布陣設計問題，但未展開研究。本文在文獻[2~4]的研究基礎上系統、綜合地研究了微陣列式加速度傳感器，根據理論研究和實驗分析，應按加速度值的大小進行微陣列式加速度傳感器的研制。

微陣列加速度傳感器的設計理論
加速度的影響因素與加速度之間呈現某種關系，應用多元回歸理論研究加速度場的數學模型，當其關系是線性時，應用線性回歸理論研究，建立數學模型及其評估方法，而為非線性時，應用非線性回歸理論

研究，建立數學模型及其評估方法。
1.1 線性回歸分析
設加速度Y與其影響因素X1, X2,…, XP存在線性關系，則其數學模型為

據此，可應用逐步線性回歸的方法，將因子一個個地引入，引入的條件是該因子的偏回歸平方和經檢驗是顯著的，同時，每引入一個因子，要對老因子逐個檢驗，將偏回歸平方和變為不顯著的因子剔除。
逐步線性回歸算法流程如下：
1) 設定函數FunInitial( )是輸入的實驗數據建立結構矩陣X、觀察值矩陣Y、自相關系數矩陣R、常數矩陣B、增廣矩陣R(0)，并且設置相應的初始化值，函數FunAssesGet( )引入因子時，計算偏回歸平方和及檢驗的函數；2) 函數FunAssesPel( )引入一個因子后，做剔除舊因子的檢驗函數；3) 數組均用首元素表示當前已被使用的數組數目；4) 數組Already Trans Row [n]記錄已經被檢驗過，放入回歸方程中的因子下標；5) 整數

變量L用來計數，對n-1次可能的引入因子的處理加以限制；6) 整數變量T, rausRow表示當前要進行R矩陣變換的行，當其值為−1，表示沒有轉化的行，程序最終輸出有效的回歸方程。
1.2 非線性回歸分析
當測試加速度與影響因素呈非線性關系，則需建立非線性模型，并應用阻尼最小二乘法解決。
1) 非線性回歸數學模型及分析方法
假設函數

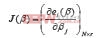同時對阻尼因子的調整作了研究，使阻尼的確定和計算速度滿足實際應用的要求。