深海底機器人行走防滑控制
比例電磁鐵控制線圈的端電壓增量方程:
δu(s)=lsδi(s)+(rc+rp)δi(s)+kesxv(s) (4)
銜鐵組件的動態力平衡方程:
kiδi(s)=mts2xv(s)+btsxv(s)+(ks+ky)xv(s)+t(s) (5)
閥芯動態力平衡方程:
t(s)=[mvs2+bvs+(kv+kfv)]xv(s) (6)
式中,l-線圈電感,h;rc,rp-線圈和放大器內阻,ω;ke-線圈感應反電動勢系數,v;ki-比例電磁鐵電流力增益,n/a;mt-銜鐵組件質量,kg;bt-阻尼系數,n·s/m;ks-銜鐵組件的彈簧剛度,n/m;mv-閥芯質量,kg;bv-閥芯的粘性阻尼系數,n·s/m;kv-閥芯對中彈簧剛度,n/m;kfv-作用于閥芯上的穩態液動力剛度系數,n/m;δi-線圈電流,a;ky-比例電磁鐵的位移力增益和調零彈簧的剛度之和,n/m;t-銜鐵外負載,n。
比例方向閥的模型框圖如圖3所示。
深海作業機器人防滑滑模變結構控制方法
(1)滑模切換函數
履帶的縱向滑轉率最好控制在略小于理想滑轉率λt的一個小區域內,以便充分發揮履帶的牽引能力,同時又能保證車輛具有一定的側向性能。在實現防滑的滑模變結構控制時,若以履帶縱向滑轉率λ作為控制目標,設控制目標理想滑轉率為λt,那么滑模變結構控制履帶過度滑轉實質上就是調節履帶實際縱向滑轉率與目標縱向滑轉率λt之間的差值,并使之趨近于零。
控制的目標是尋找驅動力矩tm的控制規律,使得滑轉率跟蹤誤差e趨向于零,設λt為海底行走最佳滑轉率,則就是最佳滑轉率對時間的導數。
假設最佳滑轉率已知,控制的目的為控制驅動力矩的輸入,使跟蹤誤差λ(t)-λt(t)趨近于零,所有狀態變量有界。
滑模控制器應用切換函數來改變tm的控制規律,定義切換函數為:
式中c1為待定系數,c1>0,e為驅動輪滑轉率的誤差變量,e=λ-λt
(2)基于μ-λ曲線形狀的λt估計
通過分析可以提出λt的搜尋方法:
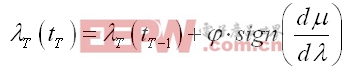 (8)
(8)式中,φ是一符號為正的步進常數,當時,λt的值增加φ,同理,當時的λt的值減少φ。這樣累計之后就能夠得到系統的最佳滑轉率。
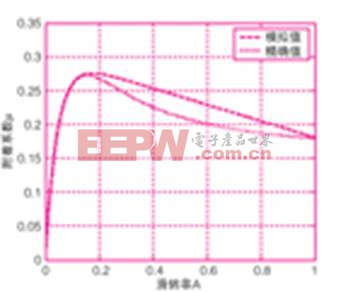
圖4 不同行駛底質附著系數-滑轉率關系圖

圖5 滑轉狀態相軌跡圖
仿真結果
(1)滑轉率辨識仿真
圖4中顯示的是深海底附著系數-滑轉率關系的擬合方法仿真結果。點虛線為根據附著系數定義由縱向牽引力得到的附著系數精確值c=2500;k=0.3;kr=0.45;a=3.25;g=50000;。劃線虛線為根據burckhardt公式得到的擬合值,c1=0.3016;c2= 23.129;c3=0.121可以看出在附著系數的上升段擬合值和精確值幾乎完全重合,該段對于最佳滑轉率的識別是最有意義的一段,所以文中所用的擬合方法有很高的準確性。
(2)滑轉率跟蹤仿真
圖5為滑轉率跟蹤控制的相軌跡圖,如圖中所示,在控制過程中,其相軌跡迅速趨于切換線,并在到達切換線之后將沿切換線快速滑向設定的理想值(λt,0),從而達到控制的要求。
結論
本文以深海作業機器人為研究對象,以車輛地面力學為基礎,分析了深海作業機器人在深海底行走的特點,并在此基礎上建立了作業機器人的動力學模型。分析了履帶防滑控制的原理,確立了以滑轉率控制為核心的控制方案。基于曲線形狀的最佳滑轉率辨識方法,根據附著系數對滑轉率的導數正負來辨識滑轉率的情況,從而推導出由可測參數馬達轉矩和履帶角加速度來間接得到導數的正負值從而辨識出最佳滑轉率值。以matlab為平臺,對液壓驅動系統進行了建模和仿真,驗證所建模型的合理性。
作者簡介
于欣(1986-) 女 碩士在讀,研究領域:人工智能,計算機控制,深海機器人等。
參考文獻
[1] 丁六懷,高宇清,簡曲,等.中國大洋多金屬結核集礦技術研究綜述[j].礦業研究與開發,2003,23(4):5~8.
[2] daegun hong, paljoo yoon. wheel slip control systems utilizing the estimated tire force. minneapolis, minnesota, usa: the 2006 american control conference, 2006.
[3] 劉志新,張大衛,李幼德,等.基于滑轉率的四輪驅動汽車防滑模糊控制仿真[j].農業機械學報,2005,36(12):21~24.
[4] 張克健.車輛地面力學[m].北京:國防工業出版社,2002.本文引用地址:http://www.104case.com/article/160151.htm











評論