基于神經網絡的恒壓供水系統設計
加入技術交流群
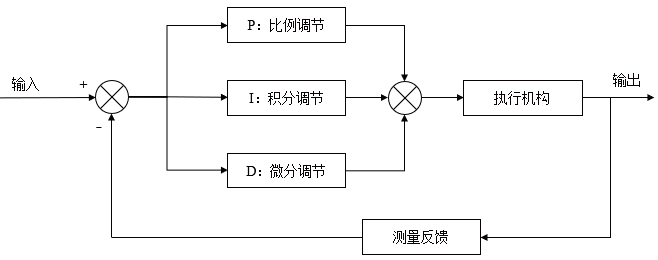
1．3 數字式PID原理
因在連續控制系統中，PID控制具有典型的結構，參數整定方便，同時伴隨計算機技術的發展，在線測量速度加快，所以PID控制器被很廣泛應用。模擬控制系統中，PID的控制規律為：
K-比例系數；Ti-積分時間常數；Td-微分時間常數
輸出控制量取決于輸入與輸出的偏差、偏差積分和偏差微分3個因素，對連續的PID控制算法進行離散處理，如采樣周期T很小，則可得到離散PID表達式：
式中，u(k)為控制器在K時刻的輸出，Ki=Ip／Ti，Kd=KpTd，T為采樣周期，K為采樣序號，K=1，2，…，e(k-1)和e(k)分別為第(K-1)和第K時刻所得的偏差信號。上式可以看出，想要計算u(k)，要本次與上次偏差信號e(k和e(k-1)，而且還要在積分項中把歷次偏差信號e(j)進行相加，即求取累加信號，因此在具體實踐中需要占用很大的存儲空間，使用起來非常不方便。為了減少計算的工作量，節約存儲空間，經常采用增量式控制算法，上式，用u(k)-u(k-1)，并進行一些變換，可得到增量式PID控制的表達式：
△u(k)=Kp(e(kT)-e(kT-T))+Kie(kT)+Kd(e(kT)-2e(kT-T)+e(kT-2T))
Kp-比例系數；Ti-調節器的積分時間；Td-調節器的微分時間
調節器改造成數字PID調節器對于工業控制過程來說，經常系統屬于非線性系統，并且有時候系統的準確模型是無法可知的，同時，在實際的生產過程當中，經常受到系統參數不穩定等多種因素的影響，系統調試比較繁瑣，并且性能欠佳，因此，人們尋求能夠自學習、自整定的技術，以適應復雜的控制系統，而神經網絡技術的發展將這種設想變成現實。
神經網絡根據系統的運行狀態調節PID控制器的參數，從而達到控制系統性能的最優化，使輸出層神經元的輸出狀態對應于PID控制器的3個可調整參數kp，ki，kd通過神經網絡的自學習，權系數調整，使神經網絡輸出對應于某種最優控制規律下的PID控制器參數。
1．4 基于BP神經網絡的PID調節器整定原理
根據數字式PID的表達式可以看出，PID調節器參數調優就是確定比例系數kp，積分時間常數ki，微分時間常數kd，使得系統滿足某些性能指標，因此，PID參數優化問題就是(kp，ki，kd)三維參數的目標優化問題。
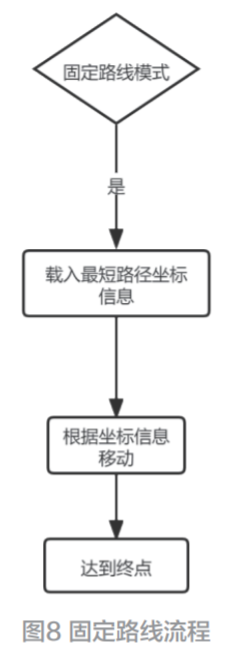
根據系統需求，采用三層BP網絡，其結構如圖3所示。本文引用地址：http://www.104case.com/article/159319.htm
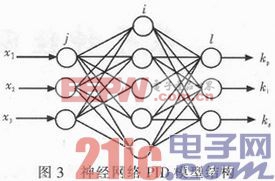
為反映輸入PID控制器信號的特性，其輸入層神經元個數選為3：x1(k)=e(k)為誤差量，
，反映誤差的累計效果，類似連續系統中的積分效果，x3(k)=e(k)-e(k-1)，反映誤差變化快慢，相當于連續系統中的微分效果。x1(k)，x2(k)和x3(k)作為輸入，能夠比較全面的反映誤差量的狀態，因此用它們來作為網絡輸入層的3個輸入量。輸出層輸出節點分別對應3個可調參數kp，ki，kd，故輸出層神經元個數為3。由于控制參數kp，ki，kd不能為負值，所以輸出層神經元的激發函數取非負的Sigmoid函數。
隱層的神經元個數可由以下經驗公式
確定式中：n，q，m分別為輸入層、隱層和輸出層神經元個數，由上式計算可得，n+m取值在2～3之間，并且公式中f可取1～10，由于網絡節點數過多會增加計算量，個數太少則不能很好地逼近給定函數，綜合考慮，此處q取5隱層神經元的激發函數取正負對稱的Sigmoid函數。
輸出層輸出節點分別對應3個可調參數kp，ki，kd。
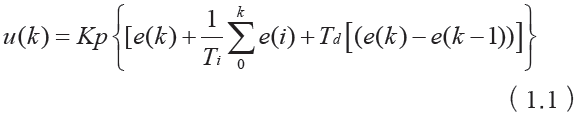
評論