Cyber15隊智能汽車競賽技術報告(節選)

　　然后，將卡爾曼濾波矩陣形式轉化為方程形式：
       
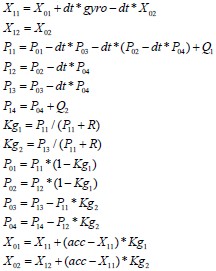
　　這里，X01即為我們需要的角度卡爾曼濾波值。

　　可以看到的是，卡爾曼濾波方程形式共有14個公式，同時很多參數的運算涉及浮點數，這對于單片機的高效運行時極為不利的，因此我們需要通過一些方法對卡爾曼濾波的公式進行化簡，從而在不失精度的情況下，盡可能減小運算量。

　　需要注意的是，Q,R兩個參數是關于傳感器和系統的方差，他們隨著系統的工作狀況不同而會產生相應變化，對應到我們的系統，在車模運行狀態不同(傾角不同，PWM不同)情況下，Q,R都是不同的。

　　根據相關參考文獻，Q,R雖然都是關于時間的變量，但是由于卡爾曼濾波有很好的收斂性，所以可以將Q，R都取比較極端的參數。用常量來定義。然后再看圖3，注意方框中的公式，根據我們的觀察，不難發現，整個方框中都是為了獲得卡爾曼增益(矩陣Kg)，我們設想，能否使用一個常數來等效替代卡爾曼增益那?根據我們在實驗中的觀察，卡爾曼增益是一個收斂的變量，并且針對到我們的這個系統，他的值非常小，直立狀態下趨近于一個常數。(所有這些工作都在MATLAB下完成)

　　所以，我們將方框中的所有公式完全省略，通過實驗整定，選取一個近似Kg來替代方框中的所有運算。同時，通過NATLAB觀測各變量的變化趨勢，我們嘗試讓Kg2=0(Kg1，Kg2本身就是非常小的變量，所以可以讓其等于0)。并發現Kg2對于整個卡爾曼濾波的影響非常有限。所以將Kg2設定為0。

　　以下就是我們組程序中卡爾曼濾波的簡化算法實現
         

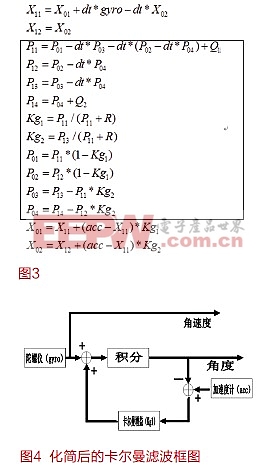
　　X1=X0+gyro*dt;
　　X0=X1+(acc-X1)*kg;
　　化簡后的卡爾曼濾波框圖如圖4。

　　卡爾曼濾波參數整定

　　化簡后的卡爾曼濾波主要是對dt以及Kg兩個參數進行整定。需要特別指出的是，這里的dt并不只是一個采樣間隔。由于陀螺儀的輸出和加速度計輸出的量綱并不相同，所以陀螺儀采樣值*dt并不直接反應一個角度，而是與實際角度相差一個系數。因此此處的dt可以等效理解為dt=采樣間隔*比例系數。

　　dt越大，積分速度越快，卡爾曼輸出追隨實際角度的情況越好(當然不能太大，不然可能會出現超前相位)。但是dt越大，陀螺儀漂移造成的影響也就越大。

　　Kg決定了加速度計的權重。Kg越大，實際輸出的漂移就越小，但是濾波效果的噪聲也就越大。

　　所以dt和kg是一對矛盾，不能太過于極端。

　　首先是靜態整定。

　　將車模保持在穩定直立狀態，讓車輪以恒定PWM(80%以上)轉動，然后調節參數。