[Machine Learning] 梯度下降法的三種形式BGD、SGD以及MBGD

來源：信息網絡工程研究中心

1. 批量梯度下降法BGD

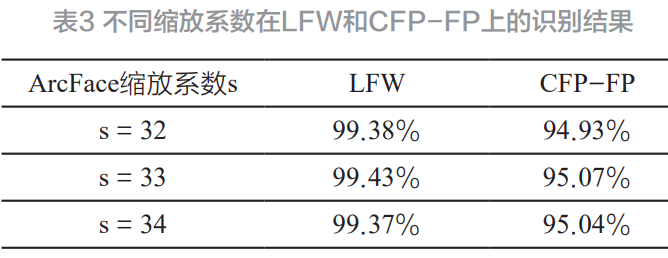
2. 隨機梯度下降法SGD

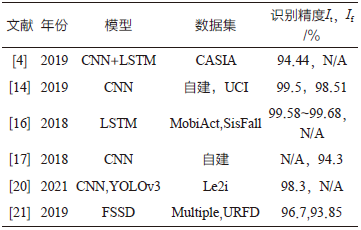
3. 小批量梯度下降法MBGD

4. 總結

在應用機器學習算法時，我們通常采用梯度下降法來對采用的算法進行訓練。其實，常用的梯度下降法還具體包含有三種不同的形式，它們也各自有著不同的優缺點。

下面我們以線性回歸算法來對三種梯度下降法進行比較。

一般線性回歸函數的假設函數為：

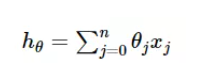
對應的能量函數（損失函數）形式為：

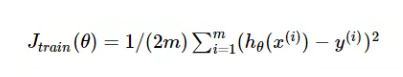
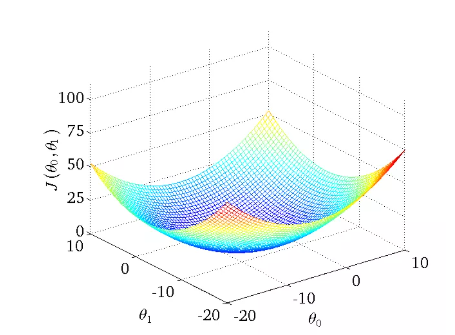
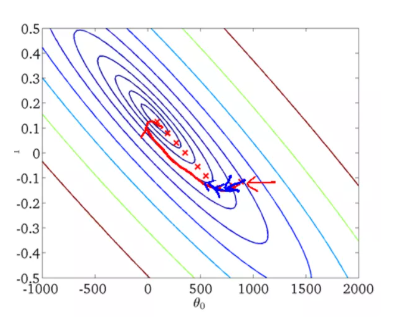
下圖為一個二維參數組對應能量函數的可視化圖：

1. 批量梯度下降法BGD

批量梯度下降法（Batch Gradient Descent，簡稱BGD）是梯度下降法最原始的形式，它的具體思路是在更新每一參數時都使用所有的樣本來進行更新，其數學形式如下：

(1) 對上述的能量函數求偏導：

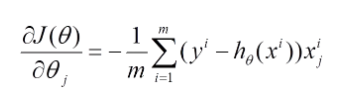
(2) 由于是最小化風險函數，所以按照每個參數θ梯度負方向來更新每個θ

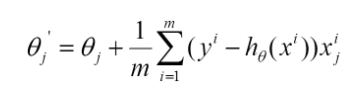
具體的偽代碼形式為：

　　repeat{　　　　

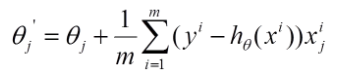
　　　　　　　　（for every j=0, ... , n）

　　}

從上面公式可以注意到，它得到的是一個全局最優解，但是每迭代一步，都要用到訓練集所有的數據，如果樣本數目m大，那么可想而知這種方法的迭代速度！所以，這就引入了另外一種方法，隨機梯度下降。

優點：全局最優解；易于并行實現；

缺點：當樣本數目很多時，訓練過程會很慢。

從迭代的次數上來看，BGD迭代的次數相對較少。其迭代的收斂曲線示意圖可以表示如下：

2. 隨機梯度下降法SGD

由于批量梯度下降法在更新每一個參數時，都需要所有的訓練樣本，所以訓練過程會隨著樣本數量的加大而變得異常的緩慢。隨機梯度下降法（Stochastic Gradient Descent，簡稱SGD）正是為了解決批量梯度下降法這一弊端而提出的。

將上面的能量函數寫為如下形式：

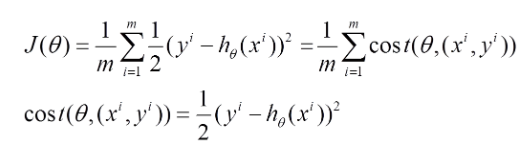
利用每個樣本的損失函數對θ偏導得到對應的梯度，來更新θ：

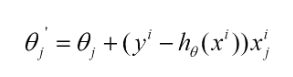
具體的偽代碼形式為：

　　1. Randomly shuffle dataset；

　　2. repeat{

　　　　for i=1, ... ,m{

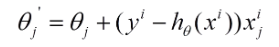
 　　　　　　(for j=0, ... ,n)

　　　　}

　　}

隨機梯度下降是通過每個樣本來迭代更新一次，如果樣本量很大的情況（例如幾十萬），那么可能只用其中幾萬條或者幾千條的樣本，就已經將theta迭代到最優解了，對比上面的批量梯度下降，迭代一次需要用到十幾萬訓練樣本，一次迭代不可能最優，如果迭代10次的話就需要遍歷訓練樣本10次。但是，SGD伴隨的一個問題是噪音較BGD要多，使得SGD并不是每次迭代都向著整體最優化方向。

優點：訓練速度快；

缺點：準確度下降，并不是全局最優；不易于并行實現。

從迭代的次數上來看，SGD迭代的次數較多，在解空間的搜索過程看起來很盲目。其迭代的收斂曲線示意圖可以表示如下：

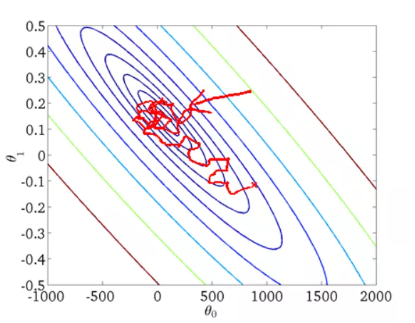
3. 小批量梯度下降法MBGD

由上述的兩種梯度下降法可以看出，其各自均有優缺點，那么能不能在兩種方法的性能之間取得一個折中呢？即，算法的訓練過程比較快，而且也要保證最終參數訓練的準確率，而這正是小批量梯度下降法（Mini-batch Gradient Descent，簡稱MBGD）的初衷。

MBGD在每次更新參數時使用b個樣本（b一般為10），其具體的偽代碼形式為：

　　Say b=10, m=1000.

　　Repeat{

　　　　for i=1, 11, 21, 31, ... , 991{

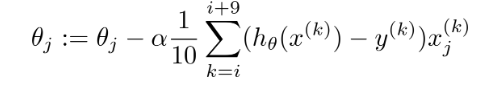
　　　　(for every j=0, ... ,n)

　　　　}

　　}

4. 總結

Batch gradient descent: Use all examples in each iteration；

Stochastic gradient descent: Use 1 example in each iteration；

Mini-batch gradient descent: Use b examples in each iteration.