同態加密算力開銷如何彌補？港科大等提出基于FPGA實現的同態加密算法硬件加速方案

當前，各行各業中的隱私泄露問題層出不窮，人們對于隱私安全保護的需求日益提高。隨著相關法律法規體系的逐漸成熟，眾多隱私計算技術也應運而生，聯邦學習就是其中的佼佼者。通過結合同態加密、秘密共享、不經意傳輸等安全計算方法，聯邦學習使得多個數據持有者，可以在保證數據安全的前提下，協同構建機器學習模型。在聯邦學習中所使用的多種隱私計算技術中，同態加密的功能和實用性舉足輕重。

在各行各業，不難想象這樣的場景，A 公司擁有大量數據，然而其并沒有人力或計算能力對這些數據進行分析處理，因此，A 公司希望購買 B 公司的計算服務對數據進行處理，但是，A 公司不希望 B 公司獲取這些數據的具體信息，因此，如果可以將數據進行加密，再傳遞給 B 公司進行處理，則可以滿足 A 公司的所有需求。因此，在這樣的場景下，我們需要一套加密體系，對密文執行的一些運算操作，可以等效為對明文執行的運算。

支持對密文進行運算操作的加密體系，被統稱為同態加密，而同態運算則泛指對密文執行的各種運算。根據密文可執行運算的范圍，同態加密算法被劃分為全同態加密、部分同態加密、近似同態加密等。一般來說，對同態運算沒有限制的加密算法被稱為全同態加密，而僅支持單一同態運算的加密算法被稱為部分同態加密。誠然，全同態加密是一種非常理想、需求巨大的算法，然而，目前主流的全同態加密算法，運算復雜度都相當之高，計算時間之漫長，使其幾乎無法在生產行業中實現落地。因此，部分同態加密成為了更加現實的解決方案。Paillier 加密就是一套被廣泛使用的部分同態加密算法，它支持密文之間的加法運算。

盡管相對于全同態加密，Paillier 加密的計算效率已經較為可觀，但是，相比較于高效的明文處理，Paillier 加密系統還是不可避免地引入了大量計算開銷。在大數據相關產業迅速發展的今天，成千上萬的數據需要得到實時處理，而傳統 CPU 的計算能力已經無法滿足需求。

FPGA（Field Programmable Gate Array），全稱為現場可編程邏輯門陣列，是一種可以根據需求對底層電路結構進行設計更新的芯片，在通信、圖像處理等領域擁有廣泛的應用。通過使用 FPGA 內部邏輯資源構建計算電路，例化大量計算引擎，可以提高計算并行度，實現對指定算法的加速計算。傳統意義上的 FPGA 開發為 RTL（Register-transfer Level）開發，開發人員通過硬件描述語言（Verilog 或 VHDL）控制寄存器讀寫、規劃時序邏輯等，描述具體的硬件功能。這種開發模式需要大量的開發經驗以及較長的硬件開發周期，并不適用于開發人員經驗不足或者亟須產出的項目開發。因此，HLS（High Level Synthesis）開發受到了很多開發者，尤其是科研工作者的青睞。HLS 是一種代碼綜合技術，開發人員可以通過高級語言（C 或 C++）描述運算，HLS 開發套件將高級語言編譯為 Verilog 或 VHDL 代碼，再生成具體網表。開發者無需關心具體硬件電路的設計，只需構造合理運算邏輯，即可在短期內完成一項 FPGA 工程。

使用 HLS 開發實現基于 FPGA 的 Paillier 加密運算，不僅可以提高計算效率，對于同態加密以及聯邦學習的硬件加速探索，也有十分重要的意義。

為了實現硬件加速，合適的算法選擇十分必要。基于二進制進行運算的芯片，包括 CPU，都可以輕松實現高效的加法、乘法、位移等運算；然而取模、除法等運算則一直是硬件電路難以啃下的硬骨頭，計算效率十分低下，顯然 Paillier 加密運算中存在不可避免的取模和冪運算。眾所周知，冪運算由若干乘法組成，而模冪運算圖片，可以由大名鼎鼎的快速冪算法拆解為若干少量的模乘運算圖片。

那么是否存在一種算法，無需單獨取模，就可以實現模乘運算呢？答案是肯定的，這個算法就是蒙哥馬利模乘算法。

圖一：蒙哥馬利模乘算法。

蒙哥馬利算法的基本思想如圖一所示，其中 l 為 M 的位寬，k 為基數，一般為 16、32、64 這樣遠小于 1024，且 FPGA 可以直接進行乘法運算的位寬。可以看到，這個算法本質上是一個二重循環，和普通的大數乘法十分相似，但是該算法通過引入參數 q，保證中間結果可以被2^k整除（被 2 的整數次冪除本質上就是向右移位），從而可以無誤差地通過移位操作完成除法，同時保證，完成了移位之后得到的最終結果一定位于區間[0,2M），從而可以通過一次數值比較和減法，將最終結果限制在[0,M），無形中完成了冪運算。基于蒙哥馬利模乘運算，再實現就成為了非常簡單的操作，實現的方法也有很多。

系統設計介紹

論文鏈接：https://arxiv.org/pdf/2007.10560.pdf

來自港科大 iSing Lab 等機構的研究者以蒙哥馬利模乘運算為核心，提出了一套基于 FPGA 的同態加密加速體系，如圖二所示，該系統被設想為部署在云服務器端，這些服務器屬于聯邦學習的參與方。該系統包括上位機 CPU 以及 FPGA，二者使用 PCIe 接口通信。CPU 負責機器學習模型的正常訓練工作，并將機器學習使用的浮點數編碼為適配同態加密方案的大整數，同時它將加密請求分批發送給 FPGA；FPGA 中為 Paillier 加密設計了高性能處理器，且硬件模塊被封裝為 OpenCL 內核由 CPU 進行調用。接下來，我們對 FPGA 內部高性能處理器的設計進行詳細介紹。

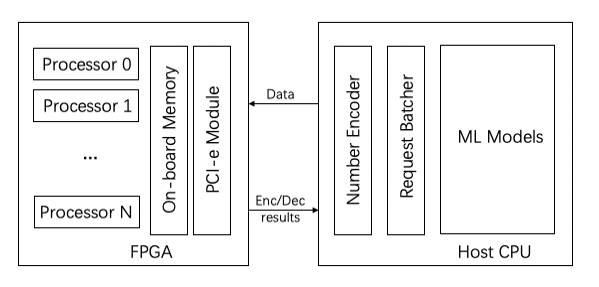
圖二：FPGA 聯邦學習加速系統。

一個 Paillier 處理器中包含了模冪、隨機數生成等所需的運算功能，此 HLS 設計中例化了若干 Paillier 處理器以實現運算的并行處理。此外，為了管理多處理器的工作，需要頂部模塊執行數據分發以及計算結果收集的工作。顯然，由于 FPGA 內部邏輯資源有限，此系統的運算效率取決于可以例化多少 Paillier 處理器，而 Paillier 處理器的主要組成部分是蒙哥馬利模乘。因此，如何在硬件上優化蒙哥馬利模乘運算成為了主要工作。我們從資源分配和時序分析兩個方面對優化工作進行介紹。

資源分配

對于一個以計算功能為主的 FPGA 工程設計中，DSP、LUT 和 RAM 是總量最有限、最需要仔細規劃使用的底層邏輯資源。DSP 是 FPGA 內部實現乘法運算不可缺少的底層邏輯資源，目前主流 FPGA 中的單個 DSP 塊，可以在高時鐘頻率下實現兩個 16 比特無符號整數之間的乘法運算，而通過串聯多個 DSP 塊，可以搭建出位寬更高的乘法器，比如，實現兩個 64 比特無符號整數之間的乘法運算需要 16 個 DSP；LUT（lookup table 查找表）是 FPGA 內部最基本的邏輯資源，我們需要結合 LUT 和其他邏輯資源構建加法器、整數比較、有限狀態機等其他邏輯電路；RAM 是 FPGA 底層集成的高速存儲器，分為 BRAM 和 URAM 兩類，一般來說，單個 RAM 可以存儲 36Kb 數據，而單個 URAM 可存儲 288Kb 數據，在當前工程中，可以使用 RAM 存放輸入輸出數據以及運算中間結果。

由圖一所示，蒙哥馬利模乘算法由內外兩重循環構成，我們將單次內部循環操作封裝為如圖三所示的處理單元，每個處理單元中包含兩個乘法器，分別用于計算 x*y 和 q*m，兩個乘法結果與外層循環的上一輪計算結果以及進位（圖中未畫出）執行加法操作。同時，為了避免 HLS 編譯代碼展開循環后，造成乘法器資源大幅膨脹，需要使用 ALLOCATION 指令將處理單元的個數限制為 1 個。

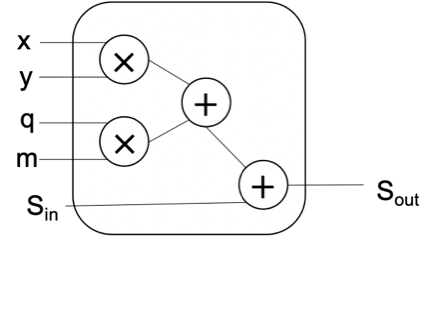
圖三：算法 1 內部循環處理單元。

圖四：Karatsuba 快速乘法。

在處理單元的設計中，同時采用了 Karatsuba 算法，如圖四所示。根據乘法運算的原理，容易看出，乘法運算操作數的位寬減半，則總計算時間將減少至原先的四分之一左右。Karatsuba 算法將整數乘法拆分為了三個位寬僅為原來一半的整數乘法，從而節省了計算時間。根據該算法的原理，可以相應地使用 DSP 資源例化出所需的乘法器。

在 RAM 的使用方面，不難注意到，用于加密的輸入數據大多是由浮點數編碼而成的，與大整數位寬相比，其有效數字很少。因此，可以將輸入數據存儲為稀疏向量，即只記錄非零元素和它們的索引，減少存儲占用。

時序分析

時序分析在 FPGA 開發中的重要性，絲毫不亞于對算法的優化以及邏輯資源的分配。從電路的角度簡單來說，如果沒有合理的邏輯設計和資源布局，不僅會使得信號傳遞時間過長，還有可能出現多組信號爭搶相同硬件資源，導致局部堵塞的問題。

通常來說，開發者可操控的最小粒度的 FPGA 工作時間為一個時鐘周期，而 FPGA 完成一個時鐘周期所需的時間由時鐘頻率決定，即

因此，在降低時鐘周期數的同時提高時鐘頻率，是提升 FPGA 運算性能的有效手段。

一般來說，實現一套算法所需要的時鐘周期數由其關鍵路徑所決定，所謂關鍵路徑，就是工作流程中，時間延遲最大的一條路徑。通過觀察蒙哥馬利模乘運算的兩重循環，可以整理出，整個運算包含次乘法，因此，如果我們例化了 n 個乘法器，每個乘法器需要運行 t 個時鐘周期，則理想中整個蒙哥馬利模乘的時鐘周期為。考慮到之前所介紹的內部循環處理單元中的兩個乘法可以并行執行，我們可以例化兩個乘法器同時進行計算；但是，由于不同的循環之間存在數據依賴關系，因此只能串行執行循環。因此，系統設計的目標是讓總時鐘周期接近。為了實現這一目標，系統中進行了以下三項優化。

展開內層循環：展開內層循環的最大好處就是將內層循環從一個單一的整體拆解為多個組成部分，從而實現多次迭代中無數據依賴部分之間的時間交疊（overlap），進而最大程度地壓縮整體運行時間。該操作可以通過 HLS 中的 UNROLL 指令實現。

將 q 的運算插入內層循環中：蒙哥馬利算法中 q 是執行內層循環的前提，但是從 q 的表達式中可以發現，只依賴于 S_i 的部分比特位，因此，當某次迭代中 S_i 的這些比特位計算完畢后，即可同時開始進行下一次迭代 q 中的計算。從而節省這部分的時間開銷。

流水線處理外層循環：通過展開內層循環，并且使用 HLS 中的 PIPELINE 指令，設置流水線初始化間隔為內層循環的迭代次數，內層循環將自動地根據拆解的操作執行流水線調度。該流水線處理示意圖如圖五所示。內層循環展開后被拆分為四個部分 S_0 ， S_1 ,  S_2 和 S_3 。當 S_0 計算完畢后，即可開啟下次迭代中 q 的計算。而 q 計算完畢后，下一次迭代計算即可開始。

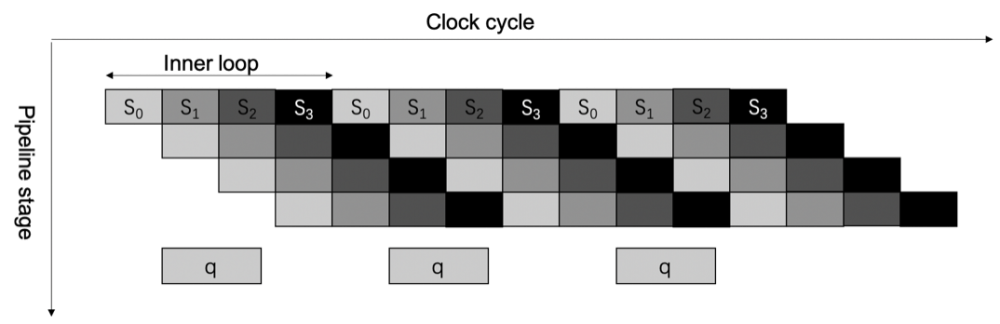
圖五：蒙哥馬利模乘運算流水線處理示意圖。

通過以上處理，不同迭代的運算操作被最大程度地交疊在一起，考慮到完成外層循環所需迭代次數較多，可以近似認為，完成整個蒙哥馬利模乘運算所需時鐘周期約為圖片。

達成時鐘周期的設計目標后，我們還希望能夠提高 FPGA 邏輯電路的時鐘頻率。盡管主流 FPGA 中的 DSP 組件的工作頻率都可以達到 400MHz 以上，但是，由于硬件資源的限制，并且考慮到系統中邏輯電路的復雜程度，將整個系統的工作頻率提高到這個數值幾乎不可能。為了盡力提高工作頻率，本系統設計中做出了如下優化：

限制乘法操作數位寬：在蒙哥馬利算法的介紹中，我們提及，基數一般選擇為 FPGA 可以輕易進行乘法運算的位寬。顯然，如果直接將選擇為 1024，FPGA 需要漫長的時間才能完成如此大位寬的乘法運算。因此，可以將限制為 32，便于掌控整個時序邏輯。

將乘法器聲明為流水（Pipelined）乘法器：流水乘法器可以將大位寬的乘法拆分到多個時鐘周期執行，從而緩解緊張的時序。簡單來說，如果我們設置系統頻率為 200MHz，乘法器幾乎不可能在一個時鐘周期，也就是 5 納秒內完成 64 比特整數之間的乘法，但是如果將乘法時間延長到 6 個時鐘周期，則乘法器則可以相對容易地在 30 納秒內完成該乘法操作。

簡化控制邏輯：這幾乎是 FPGA 開發中不可缺少的優化操作了，通過縮短邏輯電路的長度，可以增加 FPGA 在更高時鐘頻率下完成信號傳遞的頻率。在本工程中，可以使用獨熱編碼（One-hot Encoding）表示狀態機的狀態，獨熱編碼可以有效提高狀態機的查詢和匹配速度，優化時序邏輯。

系統性能測試

完成硬件設計后，通過使用 OpenCL API，上位機可以調用 FPGA 實現運算的硬件加速。我們使用 FPGA 硬件加速內核分別構建了 Paillier 加密和解密運算算子，并對比了它們和 CPU 的運算性能，其中 CPU 的運算通過調用 Paillier 運算庫 PHE 實現，對比結果如圖六和圖七所示。當公鑰位寬為 1024 比特時，FPGA 加速系統在加解密運算中分別實現了 10.62 倍和 2.76 倍的加速比。

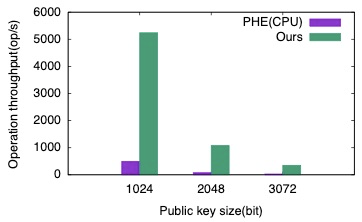
圖六：FPGA 和 CPU 加密性能對比。    

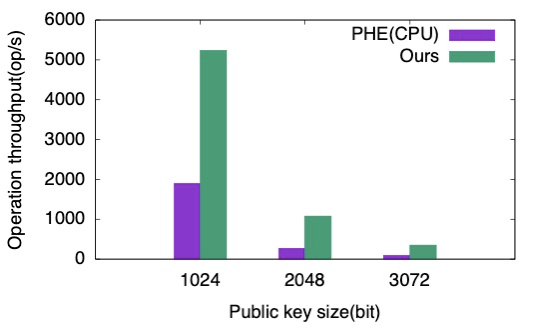
圖七：FPGA 和 CPU 解密性能對比。

將 FPGA 硬件加速集成到主流聯邦學習框架 FATE 中后，我們也看到了不錯的性能提升。我們使用 PyOpenCL API 將 FPGA 硬件加速功能集成為單一模塊，嵌入到 FATE 中執行加密運算。分別執行十次邏輯回歸迭代和十次線性回歸迭代后，我們得到了圖八所示的測試結果：FPGA 加速 FATE 削減了原始 FATE 中 71.2% 的加密時間。

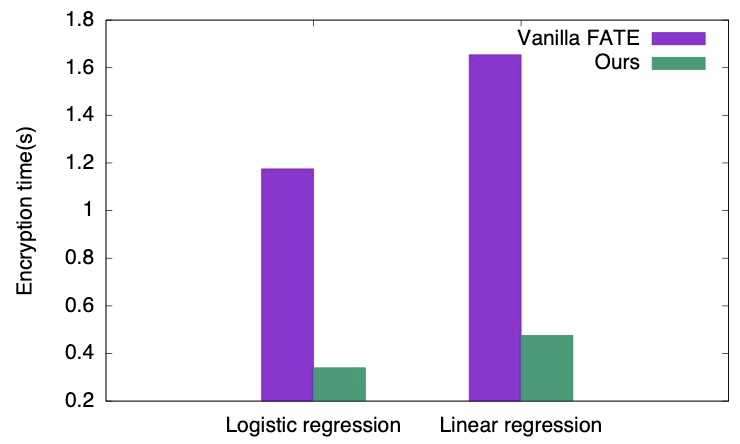
圖八：單次訓練迭代中 FPGA 加速 FATE 和原始 FATE 的加密時間對比。

總結及展望

同態加密是一種強有力的隱私保護技術，對于它們的探索，是近年來炙手可熱的研究方向；FPGA 是一種資源豐富的運算處理芯片，對于高并行度的計算任務可以帶來顯著的性能提升。對于高性能 FPGA 工程的追求，在當前階段還是難以擺脫長期的 RTL 開發。通過使用 HLS 快速開發基于 FPGA 的同態加密工程，是對 FPGA 在隱私安全計算行業進行角色定位的有效探索與嘗試。近年來，FPGA 的主流供應商 Xilinx 和 Intel 在可編程硬件的高級語言開發上不斷增加投入，FPGA 的入手難度也逐漸降低。相信隨著數據安全重要性的不斷提升，工業界將浮現出更多基于 FPGA 的安全計算產品，而類似于 HLS 的硬件上層開發模式，也將在這個領域逐漸占據一片天地。

本文作者為香港科技大學 iSing Lab 楊照雄、胡水海、陳凱。iSing Lab 是一所專注于高性能數據中心網絡、機器學習系統以及聯邦學習框架研究的實驗室。近 5 年時間中，該實驗室在網絡系統領域頂級會議 ACM SIGCOMM 和 USENIX NSDI 等定會發布論文 10 篇，根據計算機科學 CSRankings 的排名, 名為亞洲第一。