一種基于軟件重采樣的頻率測量方法

引言

　　頻率是電力系統提供電能質量的重要技術指標之一，頻率測量是電力系統運行、控制和調節的基礎。當前，電力系統中頻率測量方法有硬件和軟件兩類。傳統的硬件測量由過零比較器、方波形成電路和計數器構成，需要增加硬件測頻電路，容易受器件零點漂移和高次諧波的影響，并且占用計算機外部中斷口。在軟件測頻算法中，目前已經提出了許多不同的頻率測最算法，它們各有優缺點。過零點算法和cross算法易受諧波和噪聲影響，它們引起的過零點變化會導致測頻誤差；最小二乘法可消除噪聲影響，但對諧波敏感；卡爾曼算法計算量大，不利于實時應用；基于傅里葉濾波的測頻算法具有較強的濾波能力，而且計算數據還可用于電壓幅值的測量，具有較好的實用性。滿足采樣定理的采樣數據經傅里葉運算就可得相應的電壓、電流有效值及相位值。但實際上即使系統正常運行，頻率也不固定，而是在額定頻率附近波動。因此，使用固定采樣頻率下的數據進行計算必會有一定的偏差，不能保證每周期所采點數為整數個，使相應的傅里葉算法也產生一定的誤差。要精確測量這些參數，減少頻率波動導致的測量誤差，就需要自動改變采樣頻率來消除其影響。

　　l基于傅里葉濾波的測頻算法

　　設電力系統的電壓模型為：

式中：Umax為基頻分量幅值；A0，A1,…為各次諧波分
量。

采樣后離散化采樣序列為：

式中：fs為系統的采樣頻率。

其DFr(離散傅里葉變換)的基波向量的實部、虛部分別為：

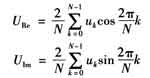
相角為：

　　若系統頻率恒定，每周期采樣后所得向量在復平面內保持不變，若系統頻率變化△f，向量在復平面內就以2π△f的角速度旋轉。因此，可通過檢測向量相角的變化，實時測出頻率的變化量，從而實時修正采樣頻率。設相鄰兩個周期的向量為z1=a1+jb1；z2=a2+jb2，頻率變化所引起的相角差為△φ，兩向量的時間間隔為T，則有△φ=2πΔfT。新的待測系統頻率為：f2=f1+Δf=f1+△φ／(2πT)。然后即可據此改變采樣頻率，跟蹤系統的實際頻率。當前所提出的各種方法大都需要改變硬件的采樣頻率，以期構成一個頻率跟蹤的負反饋系統，這樣無形中增加了系統的復雜性。以下討論一種軟件重采樣的方法，同樣達到了改變采樣頻率的目的。 2軟件重采樣的實現

　　重采樣技術是從一種數字信號采樣得到另一種數字信號，可以用專門的硬件實現，也可以用軟件方法實現，這對于提高系統的可靠性和縮短開發周期都是有利的。應用軟件重采樣技術還可以有效地降低定時采樣信號在頻域變換中產生的頻譜泄露現象，這對后繼的數據分析也是有好處的。

　　設有一個周期的采樣序列：

　　　采樣頻率為f通常為工頻的整數倍。設前一周期的測量頻率為．f，本周期與前一個周期的相角差為△φ，以此相角差修正測量頻率為f=f′+Δf=f′+△φ(2πT)。由于傅里葉算法的頻率分辨率為．fs／N，為了使傅里葉算法的基頻落在．f上，既可以改變用于計算的點數N，也可以改變fs，但由于Ⅳ為整數，其引起的誤差必然比改變．fs的誤差要大，因此，我們選擇改變fs。

　　此時可將下一個周期的采樣頻率改為Ⅳ廠，因而在不改變硬件采樣頻率的情況下對此序列進行重采樣，兩個采樣點之間的時間間隔為1／(Nf)，設第i個點將落在原硬件采樣序列的第k和k+1個點之間，其中k=「i(fs／(Nf)」，對其進行線性插值，則第i個點的值為：

　　由此得到一個新的采樣序列u′，對新序列進行傅里葉運算，并利用此算法得到的相角對頻率進行修正即可。

　　對于多通道數據采集來說，由于各個獨立通道問的初始相角不一致或頻率變化不同，各通道間重采樣后的起始周期位置各不相同，即它們的每個周期的起始時問點是不一致的，這對于需要多個通道數據進行計算的電量來說是不允許的，如功率的計算，因此必須將其時間點折算到同一點。設重采樣后的結束點落在原采樣序列中的點為k，當前測得的頻率為．f，本周期的初始相角為Φ則歸算到第1點的相角Φ′=Φ一(N一k)／(N×2π)；同樣，將另一個通道也歸算到同一個時間點即可進行計算。 當基波頻率偏離默認頻率較多時，由于傅里葉算法的頻率分辨率為fs／N，增大計算的采樣點數就可以有更小的頻率分辨率，因此，為了更快地確定本采樣序列的基頻，可以增大第1次計算時的采樣點數，在此基礎上進行頻率跟蹤。

　　3算法仿真

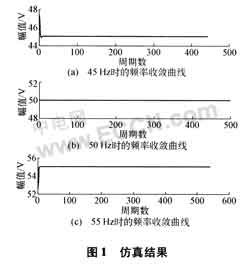
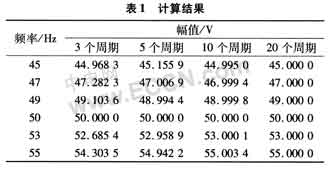
　　為估計算法的計算誤差和驗證算法的可行性，對算法進行了離線仿真計算。仿真計算結果如圖1及表l所示。

　　本文提出的應用軟件重采樣的實時測頻算法抗干擾能力強、測量精度高、動態跟蹤速度快，對電力系統頻率的各種動態過程適應性強，可廣泛應用于相量或頻率測量裝置中。數值仿真結果表明，其測量精度完全滿足安全自動裝置的要求。且該算法不需要任何附加的硬件測頻電路，已成功地應用于我們研制的微機型故障錄波裝置中，具有較好的實用價值。