基于SOPC的高精度超聲波雷達測距系統設計
上述經卡爾曼濾波算法優化后的數據會送到LCD液晶屏顯示,一部分數據顯示為實時數值數據,另一部分則先存儲,然后在LCD液晶屏的指定區域顯示為實時波形數據。
本文引用地址:http://www.104case.com/article/281893.htm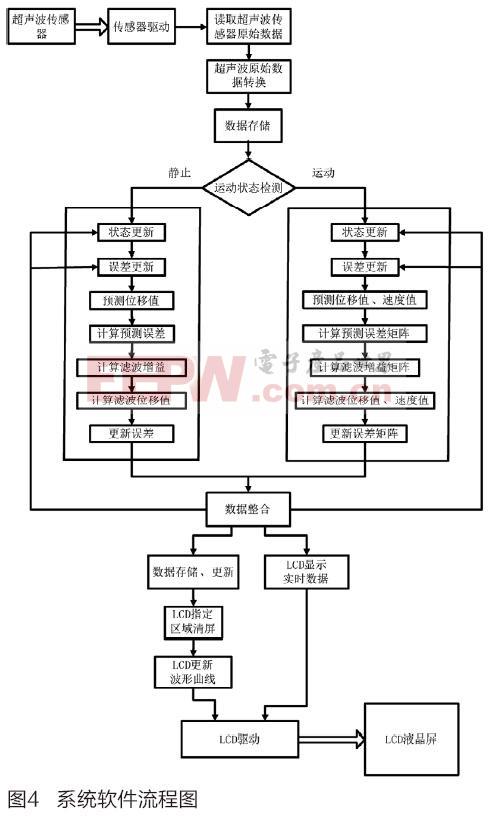
4 濾波參數設置
當系統檢測到物體處于靜止狀態時,利用一維卡爾曼濾波算法進行濾波去噪;當系統檢測到物體處于運動狀態時,則采用多維卡爾曼濾波算法,由于我們采用的超聲波傳感器的測量范圍較小,在短距離變化內,我們可以將運動物體近似看成勻速運動,所以對于運動物體,采用二維卡爾曼濾波算法進行濾波去噪。根據實際系統的噪聲和系統調試情況,一維濾波模型和二維濾波模型的系統參數設置如表1所示,其中 為采樣時間間隔,由于該系統無額外控制量,所以考慮設計控制矩陣B為零矩陣。
5 應用結果
5.1 輸入測量值分析
圖5是系統的輸入測量值,被測量物體首先處于運動狀態,由于系統噪聲和測量噪聲干擾,從該圖中可以看到實際測得的物體距離值存在較嚴重的噪聲干擾,上下波動比較大。
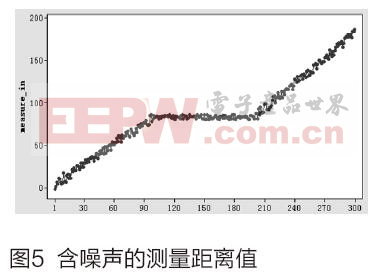
隨后物體處于靜止狀態,繼而又處于運動狀態,我們可以看到在檢測過程中,物體距離測量值都有較大的噪聲干擾,波動較大,我們使用卡爾曼濾波算法的目的就是對測量值進行去噪處理,以提高系統的測量精度。
5.2 濾波輸出數據分析
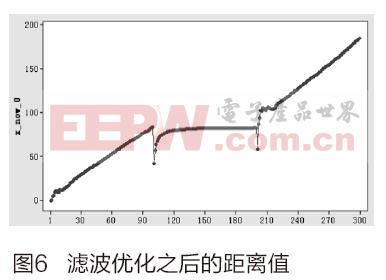
圖6是經過卡爾曼濾波算法濾波之后的距離數據。卡爾曼濾波算法在工作中,需要一定次數的算法迭代過程才能實現數據收斂,即達到較好的濾波效果。由圖6可以看到每當物體運動狀態轉換后,在經過一定次數的濾波算法迭代后,數據都能達到很好的去噪和收斂效果,對比圖5含噪聲的測量數據,在精度上有大幅提高。
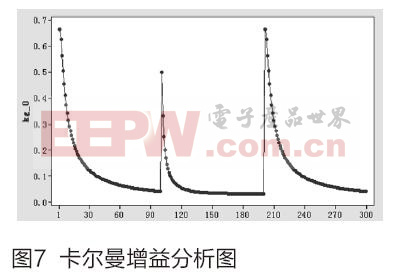
卡爾曼增益可以用來衡量卡爾曼濾波算法在工作過程中的去噪效果,在實際的濾波系統中,卡爾曼濾波增益會隨著迭代次數的增加而成指數下降,以此來實現濾波去噪的效果。圖7展示的是卡爾曼增益的變化過程,我們可以看到在每次運動狀態轉換后,卡爾曼增益都會快速下降,以使數據收斂。

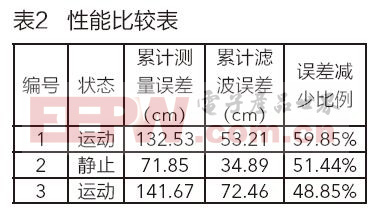
5.3 性能數據分析
表2列出了該系統對測量數據進行濾波處理的性能分析,當系統數據收斂后,我們對數據進行統計整理并列于表2中。由表2可以看出,該系統對噪聲有很好的濾波效果,可以大大提高系統的測量精度。
6 總結
利用本文提出的設計方法設計實現的超聲波雷達測距系統,結合了軟件設計方法和硬件設計方法的優勢,可以高性能的完成距離的測量,同時,卡爾曼濾波算法的引入,提升了系統的抗干擾能力,大大提高了系統的測量精度。
參考文獻:
[1]栗素娟, 朱清智, 閻保定. 基于NiosⅡ的機器人視覺伺服控制器的研究與設計[J]. 電子設計應用, 2007, (6):104-105
[2]方茁, 彭澄廉, 陳澤文. 基于NIOS的SOPC設計[J]. 計算機工程與設計, 2004, 25(4):504-507
[3]王銳, 雷金奎. 基于軟核Nios II的SOPC數據采集系統的設計[J]. 計算機測量與控制, 2008, (8)
[4]唐思章, 黃勇. SoPC與嵌入式系統軟硬件協同設計[J]. 單片機與嵌入式系統應用, 2005, (12):5-8
[5]Auger F, Hilairet M, Guerrero J M, et al. Industrial Applications of the Kalman Filter: A Review[J]. Industrial Electronics IEEE Transactions on, 2013, 60(12): 5458-5471
[6]Welch G,Bishop G. An Introduction to the Kalman Filter[J]. University of North Carolina at Chapel Hill, 1995







評論