傅立葉變換、拉普拉斯變換、Z變換最全攻略
1.傅里葉級(jí)數(shù)
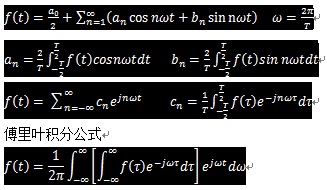
2.非周期傅里葉變換和逆變換

傅里葉變換的性質(zhì)


3.非周期序列傅里葉變換
1.定義
一個(gè)離散時(shí)間非周期信號(hào)與其頻譜之間的關(guān)系,可用序列的傅里葉變換來(lái)表示。若設(shè)離散時(shí)間非周期信號(hào)為序列x(n),則序列x(n)的傅里葉變換(DTFT)為:
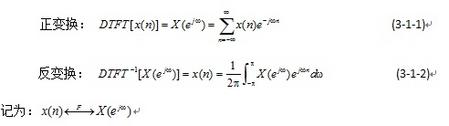
當(dāng)然式(3-1-2)等式右端的積分區(qū)間可以是(0,2π)或其它任何一個(gè)周期。
2.離散時(shí)間序列傅里葉變換存在的條件:
離散時(shí)間序列x(n)的傅里葉變換存在且連續(xù)的條件為x(n)滿足絕對(duì)可和。即:
反之,序列的傅里葉變換存在且連續(xù),則序列一定是絕對(duì)可和的。
表3-1給出了常用序列的傅里葉變換,這在以后的實(shí)際應(yīng)用中很重要。
3.1.2 非周期序列傅里葉變換的性質(zhì)
從序列傅里葉變換定義式(3-1-1)可知,非周期序列的傅里葉變換就是序列的z變換在單位圓上的取值(當(dāng)序列的z變換在單位圓上收斂時(shí)),即:
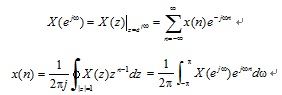
因此,非周期序列傅里葉變換的一切特性,皆可由z變換得到。正因如此,下面所述的性質(zhì),讀者可仿z變換性質(zhì)的證明方法進(jìn)行證明,在這里就不一一證明了。

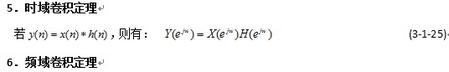

表3-1序列的傅里葉變換的性質(zhì)
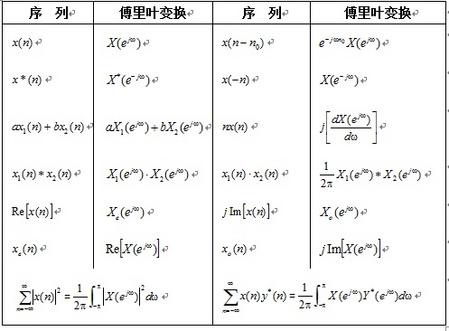
表3-2 常用序列傅里葉變換

4.拉普拉斯變換
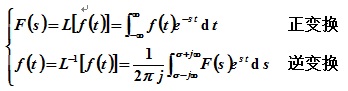
附錄A 拉普拉斯變換及反變換
1. 表A-1 拉氏變換的基本性質(zhì)
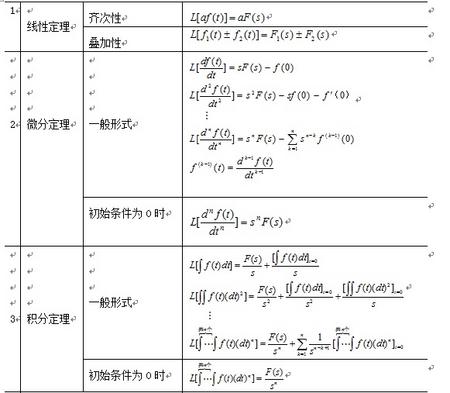

2.表A-2 常用函數(shù)的拉氏變換和z變換表

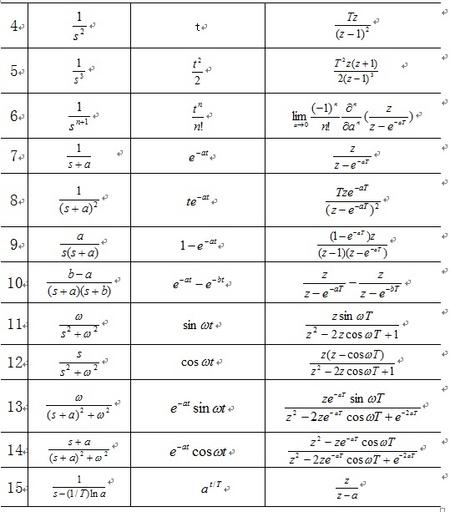
5. Z變換
1 Z變換的定義

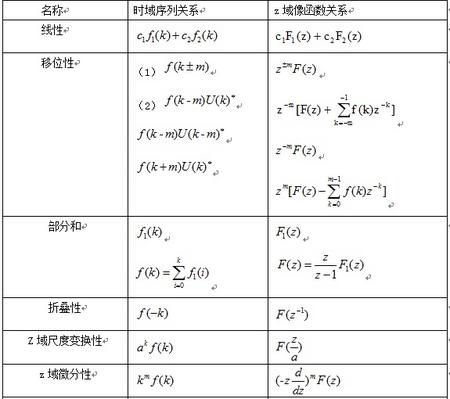
常用z變換的基本性質(zhì)和定理






評(píng)論