- 傅里葉變換在物理學、數論、組合數學、信號處理、概率論、統計學、密碼學、聲學、光學、海洋學、結構動力學等領域都有著廣泛的應用(例如在信號處理中,傅里葉變換的典型用途是將信號分解成幅值分量和頻率分量)。
傅里葉變換能將滿足一定條件的某個函數表示成三角函數(正弦和/或余弦函數)或者它們的積分的線性組合。在不同的研究領域,傅里葉變換具有多種不同的變體形式,如連續傅里葉變換和離散傅里葉變換。
傅里葉變換是一種解決問題的方法,一種工具,一種看待問題的角度。理解的關鍵是:一個連續的信號可以看作是一個個小
- 關鍵字:
傅里葉變換 拉普拉斯變換
- 簡介:本文介紹了在實際工程中常用到的傅里葉變換和Z變換之間的關系、各自的意義等內容。
傅里葉變換在物理學、數論、組合數學、信號處理、概率論、統計學、密碼學、聲學、光學、海洋學、結構動力學等領域都有著廣泛的應用(例如在信號處理中,傅里葉變換的典型用途是將信號分解成幅值分量和頻率分量)。
傅里葉變換能將滿足一定條件的某個函數表示成三角函數(正弦和/或余弦函數)或者它們的積分的線性組合。在不同的研究領域,傅里葉變換具有多種不同的變體形式,如連續傅里葉變換和離散傅里葉變換。
傅里葉變換是一種
- 關鍵字:
傅里葉變換 拉普拉斯變換 變換
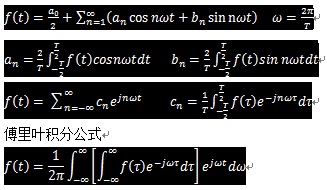
- 傅立葉變換、拉普拉斯變換、Z變換的聯系?他們的本質和區別是什么?為什么要進行這些變換。研究的都是什么?從幾方面討論下。
這三種變換都非常重要!任何理工學科都不可避免需要這些變換。
傅立葉變換,拉普拉斯變換,Z變換的意義
【傅里葉變換】在物理學、數論、組合數學、信號處理、概率論、統計學、密碼學、聲學、光學、海洋學、結構動力學等領域都有著廣泛的應用(例如在信號處理中,傅里葉變換的典型用途是將信號分解成幅值分量和頻率分量)。
傅里葉變換能將滿足一定條件的某個函數表示成三角函數(正弦和
- 關鍵字:
傅立葉變換 拉普拉斯變換
拉普拉斯變換介紹
拉普拉斯變換(英文:Laplace Transform),是工程數學中常用的一種積分變換。
如果定義:
f(t),是一個關于t,的函數,使得當t<0,時候,f(t)=0,;
s, 是一個復變量;
mathcal 是一個運算符號,它代表對其對象進行拉普拉斯積分int_0^infty e^ ,dt;F(s),是f(t),的拉普拉斯變換結果。
則f(t),的拉 [
查看詳細 ]
關于我們 -
廣告服務 -
企業會員服務 -
網站地圖 -
聯系我們 -
征稿 -
友情鏈接 -
手機EEPW
Copyright ?2000-2015 ELECTRONIC ENGINEERING & PRODUCT WORLD. All rights reserved.
《電子產品世界》雜志社 版權所有 北京東曉國際技術信息咨詢有限公司

京ICP備12027778號-2 北京市公安局備案:1101082052 京公網安備11010802012473