傅立葉變換、拉普拉斯變換、Z變換最全攻略
傅里葉變換簡單通俗理解就是把看似雜亂無章的信號考慮成由一定振幅、相位、頻率的基本正弦(余弦)信號組合而成,傅里葉變換的目的就是找出這些基本正弦(余弦)信號中振幅較大(能量較高)信號對應的頻率,從而找出雜亂無章的信號中的主要振動頻率特點。
定義式:設有一時間函數f(t) [0,∞] 或 0≤t≤∞單邊函數 ,其中,S=σ+jω 是復參變量,稱為復頻率。左端的定積分稱為拉普拉斯積分,又稱為f(t)的拉普拉斯變換;
右端的F(S)是拉普拉斯積分的結果,此積分把時域中的單邊函數f(t)變換為以復頻率S為自變量的復頻域函數F(S),稱為f(t)的拉普拉斯象函數。
以上的拉普拉斯變換是對單邊函數的拉普拉斯變換,稱為單邊拉普拉斯變換。
如f(t)是定義在整個時間軸上的函數,可將其乘以單位階躍函數,即變為f(t)ε(t),則拉普拉斯變換為F(s),=mathcal left =int_ ^infty f(t),e^ ,dt
其中積分下標取0-而不是0或0+ ,是為了將沖激函數δ(t)及其導函數納入拉普拉斯變換的范圍。
z變換可將分散的信號(現在主要用于數字信號)從時域轉換到頻域。作用和拉普拉斯變換(將連續的信號從時域轉換到頻域)是一樣的。
拉普拉斯變換是將時域信號變換到“復頻域”,與傅里葉變換的“頻域”有所區別。
FT[f(t)]=從負無窮到正無窮對[f(t)exp(-jwt)]積分 ,LT[f(t)]=從零到正無窮對[f(t)exp(-st)]積分 ,(由于實際應用,通常只做單邊拉普拉斯變換 ,即積分從零開始) .具體地,在傅里葉積分變換中,所乘因子為exp(-jwt),此處,-jwt顯然是為一純虛數;而在拉普拉斯變換 中,所乘因子為exp(-st),其中s為一復數:s=D+jw,jw是為虛部,相當于Fourier變換中的jwt,而D則是實部,作為衰減因子,這樣就能將許多無法作Fourier變換的函數(比如exp(at),a>0)做域變換。 拉普拉斯變換 主要用于電路分析,作為解微分方程的強有力工具(將微積分運算轉化為乘除運算)。但隨著CAD的興起,這一作用已不怎么受重視了,但關于其收斂域的分析(零極點圖)依然常用。 Fourier變換則隨著FFT算法(快速傅立葉變換)的發展已經成為最重要的數學工具應用于數字信號處理領域。
而Z變換,簡單地說,就是離散信號(也可以叫做序列)的拉普拉斯變換 ,可由抽樣信號的拉普拉斯變換 導出(如果你想要更多,我可以導給你看),表示式如下:
ZT[f(n)]=從n為負無窮到正無窮對[f(n)Z^(-n)]求和 ,其所變換的域稱之為“Z域”。
傅立葉變換是拉普拉斯變換的一種特例,在拉普拉斯變換中,只要令Re[s]=1,就得到傅立葉變換。當然,兩者可以轉換的前提是信號的拉普拉斯變換的收斂域要包含單位圓(即包含圓周上的點)。
很多信號都不一定有傅立葉變換,因為狄力克雷條件比較苛刻,而絕大多數信號都有拉普拉斯變換。故對于連續信號,拉普拉斯變換比傅立葉變換用得更廣泛。
兩者的共同點:都把時域函數轉換為頻域函數(對于拉普拉斯變換來說,是轉到復頻域上)。另外,兩者都能很方便地解出低階微分方程。
這三種變換的本質是將信號從時域轉換為頻域。傅里葉變換的出現顛覆了人類對世界的認知:世界不僅可以看作雖時間的變化,也可以看做各種頻率不同加權的組合。舉個不太恰當的例子:一首鋼琴曲的聲音波形是時域表達,而他的鋼琴譜則是頻域表達。
三種變換由于可以將微分方程或者差分方程轉化為多項式方程,所以大大降低了微分(差分)方程的計算成本。
另外,在通信領域,沒有信號的頻域分析,將很難在時域理解一個信號。因為通信領域中經常需要用頻率劃分信道,所以一個信號的頻域特性要比時域特性重要的多。
具體三種變換的分析(應該是四種)是這樣的:
傅里葉分析包含傅里葉級數與傅里葉變換。傅里葉級數用于對周期信號轉換,傅里葉變換用于對非周期信號轉換。
但是對于不收斂信號,傅里葉變換無能為力,只能借助拉普拉斯變換。(主要用于計算微分方程)
而z變換則可以算作離散的拉普拉斯變換。(主要用于計算差分方程)
從復平面來說,傅里葉分析直注意虛數部分,拉普拉斯變換則關注全部復平面,而z變換則是將拉普拉斯的復平面投影到z平面,將虛軸變為一個圓環。(不恰當的比方就是那種一幅畫只能通過在固定位置放一個金屬棒,從金屬棒反光才能看清這幅畫的人物那種感覺。)
全息投影相關文章:全息投影原理



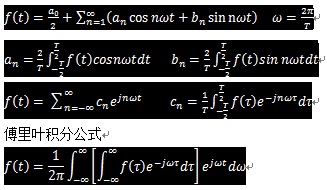

評論