一種有效的異質多傳感器異步量測融合算法

　　在條件1下，根據偽系統模型(1)，(10)，通過求解給定偽測量條件下關于目標狀態的概率密度函數推導出相應的并行濾波異步數據融合算法：

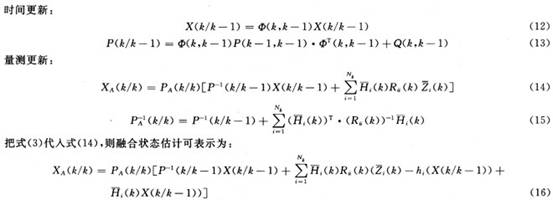
　　則式(12)～(16)構成了異質多傳感器擴維濾波融合算法，從中可知，該異步數據融合算法，計算較為簡便，但其是在條件1下的濾波融合，故該算法在性能上為次優。

　　5仿真分析

　　假設采用雷達(測量值為斜距，方位角和俯仰角)和紅外(方位角和俯仰角)2個傳感器同時跟蹤1個目標，設勻速直線運動目標的初始狀態向量為x(0)=[30 000，-200，20 000，150，1 000，10]T，測量周期為T1=T2=2 s，傳感器2比傳感器1晚1 s開始采樣，雷達和紅外傳感器的測距、測方位和測俯仰的精度為：σr=100 m，σa1=7 mrad，σa2=6 mrad，σe1=2 mrad，σe2=1 mrad，進行100次Monter Carlo仿真實驗，采用濾波RMSE的均值Ps來度量各融合算法的估計精度，且：

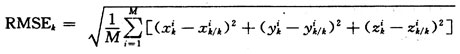
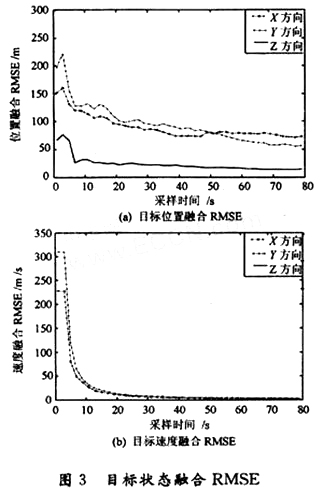
　　仿真結果如圖3所示。

　　6結語

　　本文提出一種不同傳感器數據的融合算法，即首先是通過建立偽量測方程得到同步化的偽量測數據，之后利用一種擴維濾波的思想得到目標狀態的最優估計，由于該算法適用與不同類型傳感器異步數據的融合，所以該算法是一種實際算法。從本文提出算法的仿真結果可以看出，目標3個方向位置和速度融合均方誤差均能得到較好的效果，且本文提出的算法是一種并行處理的思想，所以數據處理的速度高，特別適用于異步數據的融合處理。