直方圖在抖動分析中的應用

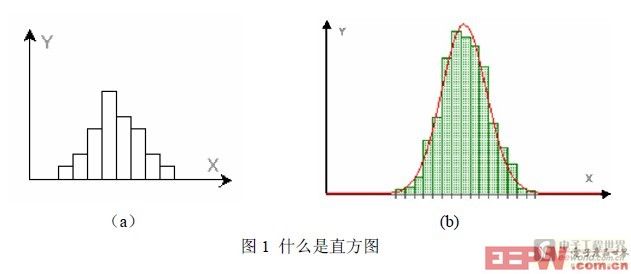
直方圖（Histogram）也叫柱狀圖，它是用一系列寬度相等、高度不等的長方形表示數據的圖，如圖1(a)所示，長方形的寬度表示數據范圍的間隔，長方形的高度表示在給定間隔內的數據數量。在統計學上這是很常用的用來表示樣本各組概率分布的一種直觀的圖表。如果樣本容量取得足夠大，分組的間隔取得足夠小，柱狀的直方圖就會變成曲線圖（圖1 b）。這條較為平滑的曲線就是樣本總體的密度曲線。它揭示了樣本的分布規律。

直方圖描繪了數據或者參數值在一個確定范圍內出現的概率（如圖2），直觀的顯示了參數的波動狀態。在用示波器對波形參數進行測量時，我們可以利用直方圖，根據測量結果的統計分析確定產品的一些關鍵指標，通過大量數據樣本的數值范圍和分布情況可以驗證產品的性能和質量并識別和診斷一些間歇性的問題。尤其是對于隨機事件（如噪聲或抖動）的了解，它是一個很好的工具。由于在抖動分析中所有信號均包含有隨機成分的抖動，因此必須采用統計的手段來分析和檢定抖動，而直方圖就是最常用的統計分析工具，所以說直方圖是抖動分析的基礎。

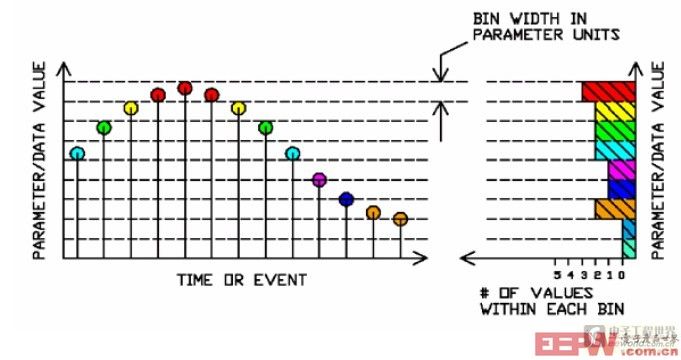
圖2 如何得到直方圖

描述直方圖的主要參數有平均值（mean）、標準偏差（standard deviation）、樣本峰-峰值和樣本總量。力科示波器包含了所有這些統計參數。

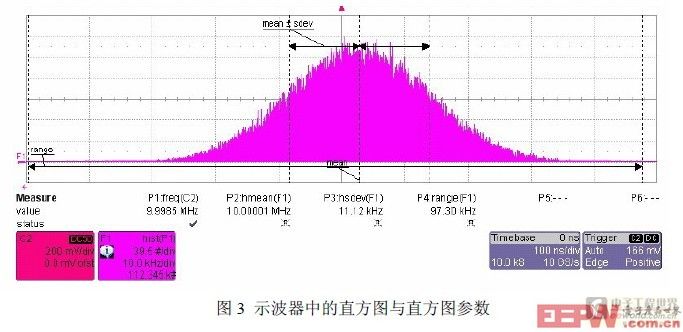
平均值是測得所有值的算術平均，表示測量值的最佳估算結果，即圖3中的“mean”。

標準偏差是測量值偏離平均值的平均量，常用σ表示。它決定了直方圖的“胖瘦”，標準偏差越大，離散程度越大，圖形就越胖。在力科示波器中用“mean ± sdev”表示直方圖的標準偏差，如果平均值為0，則標準偏差等于參數的均方根值（rms）。