微捷碼Talus TCL界面實(shí)現(xiàn)復(fù)雜分區(qū)平面布局
第V章:Zigzag緩沖區(qū)技巧
隨著設(shè)計(jì)中宏數(shù)量的增多,它通常會(huì)不斷在布局中創(chuàng)建狹長通道,且那些通道有可能在布局中被阻擋。我們常在堆疊的macro附近發(fā)現(xiàn)Zigzag緩沖區(qū)。Zigzag緩沖區(qū)意味著一個(gè)緩沖區(qū)的輸入輸出方向發(fā)生了小角度的旋轉(zhuǎn),它會(huì)帶來了總線長的增加,這對(duì)布線和時(shí)序來說都極為不利。基本上,它算是個(gè)設(shè)置得不好的緩沖區(qū)。我們不會(huì)想在我們的設(shè)計(jì)中看到它們。例如:

圖11: Zigzag緩沖區(qū)
在圖11中,紅箭頭顯示了一個(gè)緩沖區(qū)的輸入輸出連線方向;綠箭頭顯示了輸入/輸出連線的飛線。兩條綠線組成一個(gè)銳角。在這個(gè)例子中,緩沖區(qū)并未改善任何問題,反而帶來了一些轉(zhuǎn)換問題。有時(shí),單使用工具是難以解決這個(gè)問題,而且反而增加了一條緩沖鏈。為解決這個(gè)問題,我們可開發(fā)腳本并有選擇地在通道中設(shè)置一些緩沖區(qū)。
該腳本要旨是找出輸入/輸出連線的飛線間銳角。既然我們知道zigzag緩沖區(qū)、驅(qū)動(dòng)單元和接收單元的坐標(biāo),那么我們就可使用類似下方的基本三角形計(jì)算方式來得出所要結(jié)論。同時(shí),這3個(gè)點(diǎn)也組成一個(gè)三角形(圖12)。根據(jù)三角函數(shù),如果我們知道一個(gè)三角形的三邊長,那么我們就能夠算出這個(gè)三角形的每個(gè)角的角度為多少:公式為:Cosθ = (a2 + b2 – c2)/2ab; Θ = acos(cosθ)/π*180
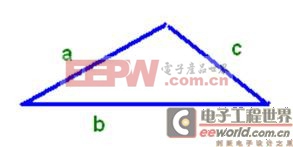
圖12:三角函數(shù)
如果Θ90 度,我們可把其視為zigzag緩沖區(qū)。這可幫助設(shè)計(jì)師在布局后快速地識(shí)別Zigzag緩沖區(qū),在進(jìn)一步優(yōu)化前正確設(shè)置好緩沖區(qū)。
總結(jié):
盡管平面布局變得困難重重、極富挑戰(zhàn)性,但好的設(shè)計(jì)分析總能使您的布局工作變得輕松些。在本文中,我們雖然分享了一些可達(dá)成這一目標(biāo)的技術(shù),但一份好的平面布局,其要求遠(yuǎn)不止這些。每份設(shè)計(jì)都有其獨(dú)特問題存在,我們應(yīng)充分利用Talus可編程界面,讓任務(wù)的完成成為可能。



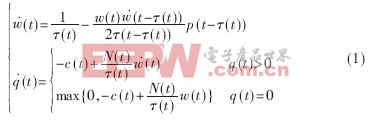

評(píng)論