前面介紹了利用根軌跡法和頻率特性法對系統進行校正。事實上,如果已知系統的模型或傳遞函數,通過引入某種控制器,使得閉環系統的極點可以移動到指定的位置,從而使系統的動態性能得到改善。這種方法稱為極點配置法。 例6-12 有一控制系統如圖6-38,其中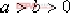 ,要求設計一個控制器,使系統穩定。 ,要求設計一個控制器,使系統穩定。
解:(1)校正前,閉環系統的極點: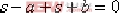 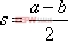 > 0 > 0
因而控制系統不穩定。 (2)在控制對象前串聯一個一階慣性環節 , c>0,則閉環系統極點: , c>0,則閉環系統極點: 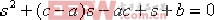
顯然,當  , ,  時,系統可以穩定。但此對參數 c 的選擇依賴于 a 、 b 。因而,可選擇控制器 時,系統可以穩定。但此對參數 c 的選擇依賴于 a 、 b 。因而,可選擇控制器 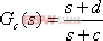 , c 、 d ,則有特征方程: , c 、 d ,則有特征方程: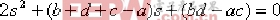 當 , , 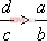 時,系統穩定。 時,系統穩定。 本例由于原開環系統不穩定,因而不能通過簡單的零極點相消方式進行控制器的設計,其原因在于控制器的參數在具體實現中無法那么準確,從而可能導致校正后的系統仍不穩定。
例6-13 已知一單位反饋控制系統的開環傳遞函數: 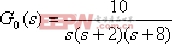
要求設計一串聯校正裝置Gc(s) ,使校正后系統的靜態速度誤差系統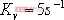 ,閉環主導極點在 ,閉環主導極點在 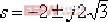 處。 處。 解:首先,通過校正前系統的根軌跡可以發現,如圖6-39所示,其主導極點為: 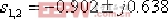 。 。
為使主導極點向左偏移,宜采用超前校正裝置。 (2)令超前校正裝置  ,可采用待定系數法確定相關參數: ,可采用待定系數法確定相關參數: 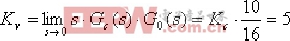
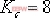
又 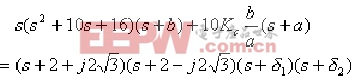
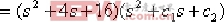
其中 、 、 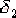 、 、 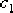 、 、 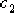 為待定系數。 為待定系數。 進一步可得: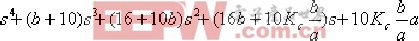  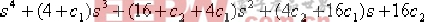
即 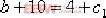 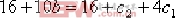
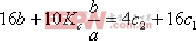
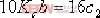
將 代入式子可以得到: , ,  , ,  , , 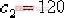 。進一步可得超前校正裝置的傳遞函數: 。進一步可得超前校正裝置的傳遞函數: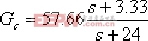 校正后系統的根軌跡如圖6-39所示。 該校正裝置與例6-7中由超前裝置獲取的校正裝置結果基本相同,說明結果是正確的。
在matlab中,亦有相應的命令可進行極點配置,主要有三個算法可實現極點配置算法:Bass-Gura算法、Ackermann算法和魯棒極點配置算法。這些算法均以狀態空間進行表征,通過設定期望極點位置,獲取狀態反饋矩陣K。下面通過示例介紹其中的一種算法。 例6-14 考慮給定的系統,其狀態方程模型如下: 
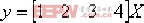 , ,
期望的閉環系統配置在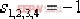 , , 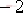 , , 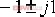 ,試設計其控制器。 ,試設計其控制器。 解:可以使用下面的MATLAB語句來實現極點的配置: A=[0,1,0,0;0,0,-1,0;0,0,0,1;0,0,11,0]; B=[0;1;0;-1]; eig(A)' ans = 0 0
pid控制器相關文章:pid控制器原理
技術專區
主站蜘蛛池模板:
子长县|
凌源市|
六安市|
永福县|
五河县|
邢台县|
同江市|
江北区|
海晏县|
桐乡市|
民丰县|
乌拉特中旗|
江孜县|
正宁县|
石台县|
保康县|
美姑县|
阿坝县|
阆中市|
绵阳市|
德保县|
兰西县|
伊金霍洛旗|
奉化市|
深水埗区|
达日县|
渝中区|
灵宝市|
鄂托克前旗|
张家港市|
凤城市|
永顺县|
普兰店市|
始兴县|
门源|
嘉祥县|
泸溪县|
陆丰市|
体育|
平定县|
池州市|
|
評論