頻率響應法-相對穩(wěn)定性分析
加入技術交流群
 |
（2）由題意得
，即
。在
處的對數(shù)幅值為
 |
上式簡化后為
 |
解之得，K＝2.5。
根據(jù)
的要求，則得
 |
即
 |
利用三角函數(shù)的性質，可求得
。于是有
 |
即
 |
求解上式得
。不難看出，K取2.5就能同時滿足
和
的要求。
5.5.3 對數(shù)幅頻特性中頻段與系統(tǒng)動態(tài)性能的關系
在分析控制系統(tǒng)的開環(huán)對數(shù)幅相頻率特性時，習慣上將頻率范圍分為三個頻段：低頻段、中頻段和高頻段。其中低頻段反映了控制系統(tǒng)的靜態(tài)特性，關于此點在5.3.4中我們作了分析；中頻段則反映了系統(tǒng)的動態(tài)特性，這是控制設計中一個非常關心的問題，這將在下面作介紹；高頻段則主要反映了系統(tǒng)的抗干擾能力，對動態(tài)性能影響不大，將不作介紹。
 |
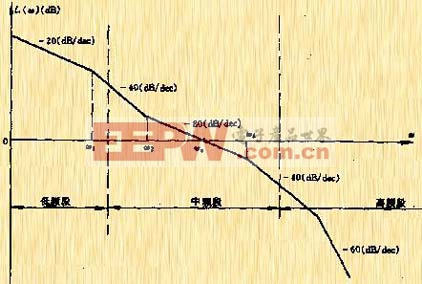| 圖5－56 對數(shù)幅頻特性三個頻段劃分 |
中頻段的主要參數(shù)有：剪切頻率
、相位裕量
和中頻寬度h。對于圖5－56所示系統(tǒng)，其中頻寬度一般定義在斜率等于
、靠近
處：
 |
|
一般要求最小相位系統(tǒng)的開環(huán)對數(shù)幅頻特性在
處的斜率等于
。如果在該處的斜率等于或小于為
，則對應的系統(tǒng)可能不穩(wěn)定，或者系統(tǒng)即使穩(wěn)定，但因相位裕量較小，系統(tǒng)的穩(wěn)定性也較差。下面通過二階系統(tǒng)和三階系統(tǒng)對上述結論進行說明。
設一標準二階系統(tǒng)的開環(huán)傳遞函數(shù)為：
 |
|
式中，自然振蕩頻率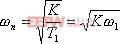
，阻尼比
，其中
為轉角頻率，則：
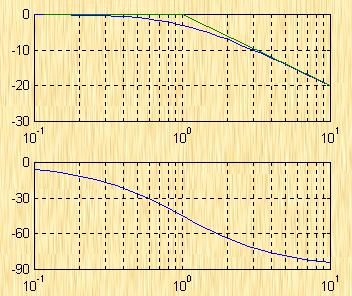
（1） 當
時，
，如圖5－57a示，階躍響應是衰減較慢的振蕩過程；
（2） 當
時，
，如圖5－57b示，階躍響應是衰減較快的振蕩過程；
（3） 當 時，
，如圖5－57c示，階躍響應是接近無振蕩的非周期過程；
 |
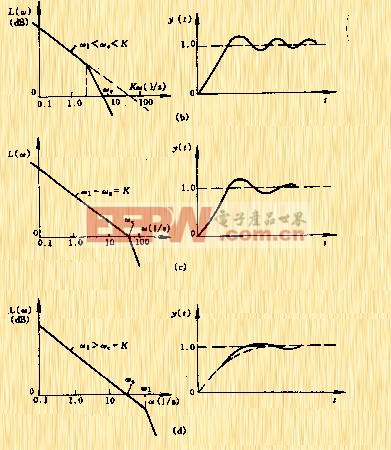| 圖5－57 二階系統(tǒng)幅頻特性和單位階躍響應 |
再設一個三階系統(tǒng)的開環(huán)傳函數(shù)為：
 |
|
取K＝0.1，1,10,100，得到如圖5－58的幅頻曲線a，b，c，d。由圖可見。當
時，式（5－59）的對數(shù)幅頻特性曲線如圖5－58所示的曲線
。剪切頻率 
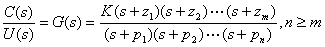
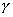
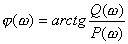
評論