頻率響應法--極坐標圖
控制系統中的時滯環節是典型的非最小相位系統。關于此點無論從它的近似展開式或其完整形式均可證明。同時從圖5-30可以明顯看出,最小相位系統的穩態誤差為零,而非最小相位系統則是發散的。因此,對于控制系統而言,相位滯后越大,系統的穩定性越差,因此應盡可能減小或避免時滯環節對控制系統的影響。
5.3.4 系統開環對數幅頻特性與閉環穩態誤差的關系
對于一定的輸入信號,控制系統的穩態誤差與系統的類型和開環放大倍數有關。在給定了系統的開環幅頻特性曲線后,即可根據其低頻段的位置或斜率確定其穩態位置誤差系數 ![]() 、速度誤差系數
、速度誤差系數 ![]() 和加速度誤差系數
和加速度誤差系數 ![]() 。對數幅頻特性的低頻段是由因式
。對數幅頻特性的低頻段是由因式 ![]() 來表征的,對于實際的控制系統,
來表征的,對于實際的控制系統, ![]() 通常為0span '>、1或2。下面分析系統的類型與對數幅頻特性曲線低頻漸近線斜率的對應關系及
通常為0span '>、1或2。下面分析系統的類型與對數幅頻特性曲線低頻漸近線斜率的對應關系及 ![]() 、
、 ![]() 和
和 ![]() 值的確定。
值的確定。
1.0型系統
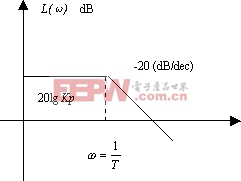 |
| 圖5-31 0型系統的對數幅頻特性 |
設0型系統的開環頻率特性為
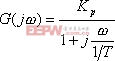 |
則其對數幅頻特性的表達式為
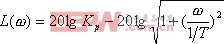 |
據此作出對數幅頻特性曲線的漸近線如圖5-31所示。由圖可見,0型系統的對數幅頻特性低頻段具有如下特點:
1) 低頻段的漸近線斜率為0 dB/dec,高度為![]() ;
;
2) 如果已知幅頻特性低頻段的高度,即可根據式:![]() 求出位置誤差系數
求出位置誤差系數 ![]() 的值,進而計算系統的穩態誤差。
的值,進而計算系統的穩態誤差。
2、I型系統
設I型系統的頻率特性為
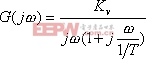 |
其對數幅頻特性的表達式為
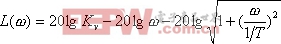 |
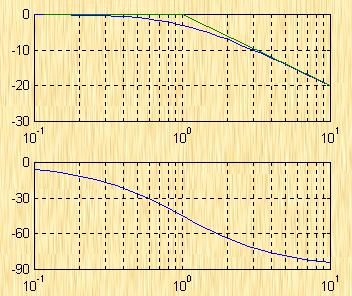
由上式作出的對數幅頻特性曲線的漸近線如圖5-32所示。
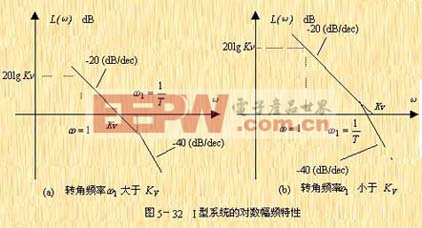 |
不難看出,I型系統的對數幅頻特性有如下的特點:
1)低頻漸近線的斜率為![]() 。
。
2)低頻段漸近線(或其延長線)在 ![]() 處的縱坐標值為
處的縱坐標值為 ![]() ,由此可求出穩態速度誤差系數
,由此可求出穩態速度誤差系數 ![]() 。
。
3)開環增益即穩態速度誤差系數![]() 在數值上也等于低頻漸近線(或其延長線)與0dB線相交點的頻率值。
在數值上也等于低頻漸近線(或其延長線)與0dB線相交點的頻率值。
3、Ⅱ型系統
設Ⅱ型系統的頻率特性
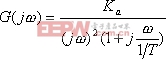 |
其對數幅頻特性的表達式為
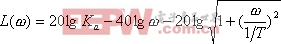 |
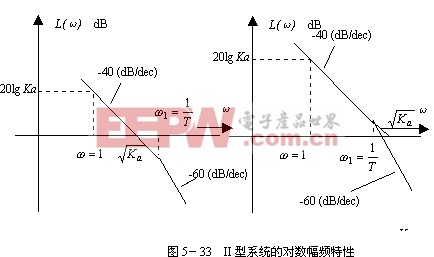
由上式作出對數幅頻特性曲線的漸近線如圖5-33所示。易知,Ⅱ型系統的對數幅頻特性有如下的特點:
1) 低頻漸近線的斜率為![]() 。
。
2)和I型系統一樣,低頻漸近線(或其延長線)在![]() 處的縱坐標值為
處的縱坐標值為 ![]() 由此可求出穩態加速度誤差系數
由此可求出穩態加速度誤差系數 ![]() 。
。
3) 系統的開環增益即加速度誤差系數![]() 在數值上也等于低頻段漸近線(或其延長線)與0dB線相交點的頻率值和平方。
在數值上也等于低頻段漸近線(或其延長線)與0dB線相交點的頻率值和平方。
 |




評論