頻率響應法--極坐標圖
加入技術交流群
隨著 
的增大而單調地減小。這意味著，當 
時，幅值曲線不可能有峰值出現，即不會產生諧振。當 
時， 
有最小值，其值為期1
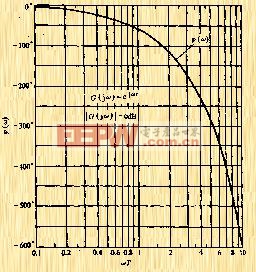
| 圖5－27 時滯系統的相頻特性 |
5.3.2 開環系統的伯德圖
設系統的開環傳遞函數為
 |
則其對應的對數幅頻和相頻特性分別為
 |
因此，只要作出
所含各環節的對數幅頻和相頻特性曲線，然后對它們分別進行代數相加，就能求得開環系統的伯德圖。
一般繪制開環系統伯德圖的步驟如下：
（1）寫出開環頻率特性的表達式，將其寫成典型環節相乘的形式。
（2）將所含各環節的轉折頻率由小到大依次標準在頻率軸上。注意，由于比例環節和積分環節沒有轉折頻率，因此可以排在最左邊。
（3）繪制開環對數幅頻曲線的漸近線。漸近線由若干條分段直線所組成，其低頻段的斜率為
，其中 
為積分環節數。在 
處， 
。以低頻段作為分段直線的起始段，從它開始，沿著頻率增大的方向，每遇到一個轉折頻率就改變一次分段直線的斜率。如遇到 
環節的轉折頻率 
，當 
時，分段直線斜率的變化量為 
；如遇到 
環節的轉折頻率 
，當 
時，分段直線斜率的變化量為 
，其它環節用類似的方法處理。分段直線最后一段是開環對數幅頻曲線的高頻漸近線，其斜率為 
，其中n為 
的零點數。
（4）作出以分段直線表示的漸近線后，如果需要，再按照前述的各典型環節的誤差曲線對相應的分段直線進行修正，就可得到實際的對數幅頻特性曲線。
（5）作相頻特性曲線。根據開環相頻特性的表達式，在低頻、中頻及高頻區域中各選擇若干個頻率進行計算，然后連成曲線。
例5-4試繪制開環系統的伯德圖 ...
已知一反饋控制系統的開環傳遞函數為
 |
試繪制開環系統的伯德圖。
解 系統的開環頻率特性為
 |
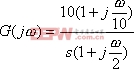由此可知，該系統是由比例、積分、微分和慣性環節所組成。它的對數幅頻特性為
 |
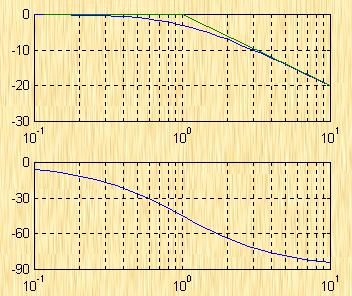
按上述的步驟，作出該系統對數幅頻特性曲線的漸近線，其特點為
1）由于
，因而漸近線低頻段的斜率為 
。在 
處，其高度為 
。
2）當
時，由于慣性環節對信號幅值的衰減任用，使分段直線的斜率由 
變為 
。同理，當 
時，由于微分環節對信號幅值的提升任用，使分段直線的斜率上升 
，即由 
變為 
。
系統的相頻特性按式：
進行計算。
上述作圖過程同樣可使用如下的Matlab語句繪制Bode圖方法。
%ex5_4
function ex5_4
G=tf(10*[0.1,1],conv([1,0],[0.5,1]));%得到傳遞函數
[x0,y0,w]=bode(G);%由Bode函數獲取幅值和相角
[x,y]=bode_asymp(G,w);%得到轉折頻率
subplot(211),semilogx(w,20*log10(x0(:)),x,y);%畫幅頻曲線和漸近線
subplot(212),semilogx(w,y0(:))%現相頻曲線
圖5-28為該系統的伯德圖。
的相位變化量為  ，系統b－29所示，相應的單位階躍響應如圖5－30。由圖可見，最小相位系統的
相關推薦
技術專區 |
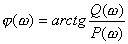
評論