控制系統的時域分析法--高階系統的暫態響應
當系統高于二階時,將其稱為高階系統。其傳遞函數一般可以寫成如下形式
 |
將上式進行因式分解,可寫成
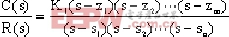 |
式中 si:傳遞函數極點,i=1、2、…、n;
zj:傳遞函數極點,j=1、2、…、m。
假定系統所有零點、極點互不相同,并假定極點中有實數極點和復數極點,而零點中只有實數零點。當輸入為單位階躍函數時,其階躍響應的象函數為
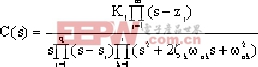 |
= + +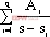 + +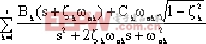 |
式中 m:傳遞函數零點總數;
n:傳遞函數極點總數,n=q+2r;
q:實極點數;
r:共軛復數極點的對數。
對上式求取原函數,即得高階系統的單位階躍響應:
c(t) = A +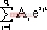 + +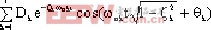 |
式中 Ai =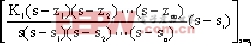 |
Dk =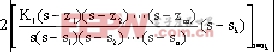 |
θk=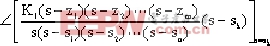 |
sk=-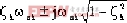 |
由此可見,高階系統的暫態響應是一階和二階系統暫態響應分量的合成。可以得到如下結論:
1.高階系統暫態響應各分量的衰減快慢由指數衰減系數si及 決定。假設系統的一對復數極點與虛軸間距離為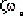 ,另一對復數極點與虛軸間距離是其5倍,即5
,另一對復數極點與虛軸間距離是其5倍,即5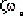 ,如按式(3-15)估算,后者對應的暫態分量衰減時間大約為前者的1/5,由此可知,系統的極點在s平面左半部距虛軸愈遠,相應的暫態分量衰減得愈快。
,如按式(3-15)估算,后者對應的暫態分量衰減時間大約為前者的1/5,由此可知,系統的極點在s平面左半部距虛軸愈遠,相應的暫態分量衰減得愈快。
2. 高階系統暫態響應各分量的系數Ai和Dk不僅與s平面中極點的位置有關,并且與零點的位置也有關。當某極點si愈靠近某一零點zj而遠離其他極點,同時與s平面的原點相距也很遠,則相應分量的系數Ai越小,該暫態分量的影響就小。若一對零、極點互相接近,則該極點對暫態響應幾乎沒有影響。極端情況,若一對零、極點重合(偶極子),則該極點對暫態響應無任何影響。若某極點si遠離零點,但距S平面原點較近,則相應的該分量的系數Ai就比較大,于是,該分量對暫態響應的影響就較大。因此,對于系數很小的分量以及遠離虛軸的極點對應的衰減很快的暫態分量常可忽略,于是高階系統的響應就可以用低階系統的響應去近似。
3. 如果高階系統中距離虛軸最近的極點,其實部比其他極點的實部的1/5還要小,并且該極點附近沒有零點,則可以認為系統的響應主要由該極點決定。這些對系統響應起主導作用的極點,稱為系統主導極點。高階系統的主導極點常是共軛復數極點。如能找到一對共軛復數主導極點,則高階系統就可以近似地當作二階系統來分析,相應地其暫態響應性能指標都可以按二階系統來近似估計。
在設計一個高階系統的時候,常利用主導極點這一概念選擇系統參數,使系統具有預期的一對共軛復數主導極點,這樣就可以近似地用二階系統的性能指標來設計系統。詳見后面有關系統設計章節的內容。









評論