控制系統常用的數學模型有三種:傳遞函數、零極點增益和狀態空間。每種模型均有連續/離散之分,它們各有特點,有時需在各種模型之間進行轉換。本節主要介紹它們的MATLAB表示及三種模型之間的相互轉換。
2.8.1連續系統數學模型的MATLAB表示 1. 傳遞函數模型 當: 則在MATLAB中,直接用分子/分母的系數表示,即
num=[b0,b1,…,bm];
den = [a0,a1,…,an]; 例2-7 用MATLAB表示傳遞函數為  的系統。 的系統。
解:在MATLAB環境下輸入
ng=[1 1]; dg=[1 3 2];
printsys(ng,dg) %此處printsys命令是傳遞函數顯示命令。
則執行后得到如下結果:
2. 零極點增益模型 當: 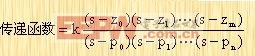 時 時 |
則在MATLAB中,用[z,p,k]矢量組表示,即
z=[z0,z1,…,zm];
p=[p0,p1,…,pn];
k=[k]; 例2-8 用MATLAB表示傳遞函數為 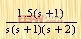 的系統。 的系統。
解:在MATLAB環境下輸入
z=-1; p=[0 -1 -2]; k=1.5;
[num,den]=zp2tf[z,p,k];
printsys(num,den) %此處printsys命令是傳遞函數顯示命令。
則執行后得到如下結果:
3. 狀態空間模型 當: 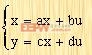 時 時 |
則在MATLAB中,該控制系統可用(a,b,c,d)矩陣組表示。 4. 傳遞函數的部分分式展開 當: 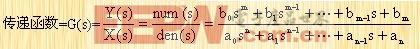 時 時 |
在MATLAB中直接用分子/分母的系數表示時有
num=[b0,b1,…,bm];
den = [a0,a1,…,an];
則命令
[r,p,k] = residue(num,den)
將求出兩個多項式Y(s)和X(s)之比的部分分式展開的留數、極點和直接項。Y(s)/X(s)的部分分式展開由下式給出: 例2-A2 考慮下列傳遞函數: 命令 [r,p,k] = residue(num,den)
將給出下列結果: [r,p,k]=residue(num,den)
r=
-6.000
-4.000
3.000
p=
-3.000
-2.000
-1.000
k=
2 留數為列向量r,極點位置為列向量p,直接項是行向量k。以下是Y(s)/X(s)的部分分式展開的MATLAB表達形式: 命令
[num,den] = residue(r,p,k)
執行后得到如下結果:
[num,den]=residue(r,p,k)
num=
2.0000 5.0000 3.0000 6.0000
den=
1.0000 6.0000 11.0000 6.0000
2.8.2離散系統數學模型的MATLAB表示 1. 傳遞函數模型: 2. 零極點增益模型: 3. 狀態空間模型: 2.8.3模型之間的轉換 同一個控制系統都可用上述三種不同的模型表示,為分析系統的特性,有必要在三種模型之間進行轉換。MATLAB的信號處理和控制系統工具箱中,都提供了模型變換的函:ss2tf,ss2zp,tf2ss,tf2zp,zp2ss,zp2tf,它們的關系可用圖2-17所示的結構來表示。  |
圖2-18 三種模型之間的轉換 |
說明: ss2tf命令:將狀態空間模型轉換成傳遞函數模型。
格式為:[num,den]=ss2tf(A,B,C,D,iu)
式中,iu為輸入的序號。轉換公式為
ss2zp命令:將狀態空間模型轉換成零極點增益模型。
格式為:[Z, P, K]=ss2zp(A, B, C, D, iu)
式中,iu為輸入的序號。
tf2ss命令:將傳遞函數模型轉換成狀態空間模型。
格式為:[A, B, C, D]=tf2ss(num, den)
tf2zp命令:將傳遞函數模型轉換成零極點增益模型。
格式為:[Z, P, K]=tf2zp(num, den)
zp2ss命令:將零極點模型轉換成狀態空間模型。
格式為:[A, B, C, D]=zp2ss(Z, P, K)
zp2tf命令:將零極點模型轉換成傳遞函數模型。
格式為:[num, den]=zp2tf(Z, P, K) 2.8.4控制系統建模 對簡單系統的建模可直接采用三種基本模型:傳遞函數、零極點增益、狀態空間模型。但實際中經常遇到幾個簡單系統組合成一個復雜系統。常見形式有:并聯、串聯、閉環及反饋等連接。 1. 并聯:將兩個系統按并聯方式連接,在MATLAB中可用parallel函數實現。命令格式為:[nump, denp] = parallel(num1, den1, num2, den2) 其對應的結果為:Gp(s)=G1(s)+G2(s) 2. 串聯:將兩個系統按串聯方式連接,在MATLAB中可用series函數實現。命令格式為:[nums, dens] = series(num1, den1, num2, den2) 其對應的結果為:Gs(s)=G1(s)+G2(s) 3. 閉環:將系統通過正負反饋連接成閉環系統,在MATLAB中可用feedback函數實現。命令格式為:[numf, denf] = feedback(num1, den1, num2, den2, sign) sign為可選參數,sign=-1為負反饋,而sign=1對應為正反饋。缺省值為負反饋。其對應的結果為: 4. 單位反饋:將兩個系統按反饋方式連接成閉環系統(對應于單位反饋系統),在MATLAB中可用cloop函數實現。命令格式為:[numc, denc] = cloop(num, den, sign) sign為可選參數,sign=-1為負反饋,而sign=1對應為正反饋。缺省值為負反饋。其對應的結果為: |
評論