為什么上升沿變緩 則輻射變小
方波的四種形式,但我們經(jīng)常遇見的是左上角和右下角的兩種形式,如圖14.4所示。
本文引用地址:http://www.104case.com/article/202411/464363.htm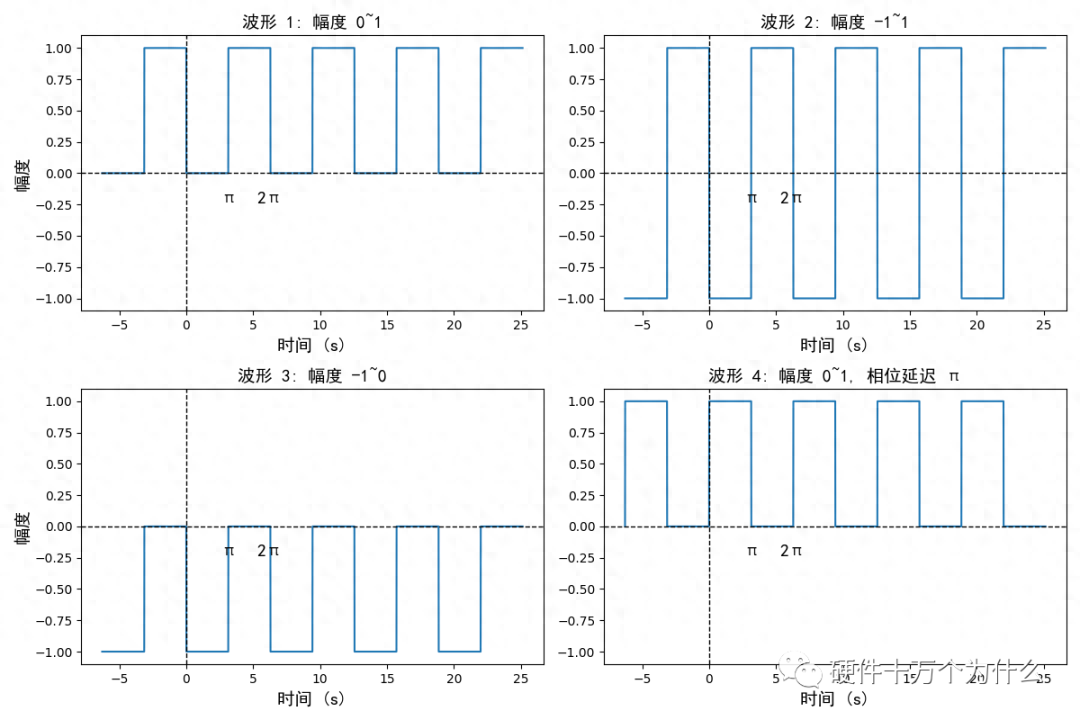
圖 14.4 四種方波波形
我們就以右下角為例來分析方波函數(shù),

我們可以把積分周期從0~T,移動(dòng)到-T/2~T/2,因?yàn)楹瘮?shù)式周期信號(hào),所以兩個(gè)區(qū)間積分的結(jié)果一致。
我們根據(jù)傅里葉級(jí)數(shù)系數(shù)公式:
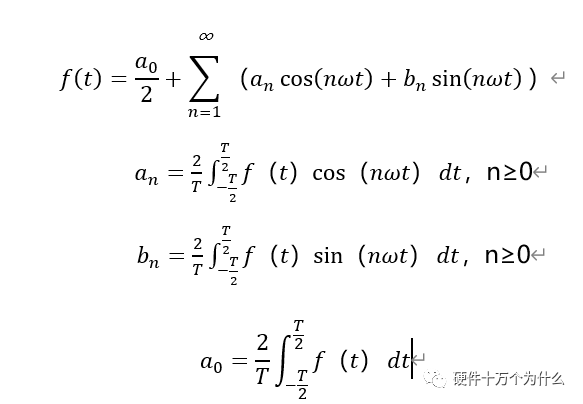




當(dāng)n為偶函數(shù)時(shí),cosnπ=1,則bn=0,當(dāng)n為奇函數(shù)時(shí),cosnπ=0,bn=2A/nπ
任何周期性的信號(hào)都可以用無數(shù)個(gè)正弦函數(shù)之和來表示,每個(gè)正弦函數(shù)分量的頻率是基頻f0=1/T的倍數(shù)。通常,噪聲也是隨著電路的運(yùn)轉(zhuǎn)而周期性地存在,因此需要對(duì)噪聲的特性進(jìn)行頻域上的分析。我們假設(shè)周期為T的方波信號(hào),波形如圖14.4所示。
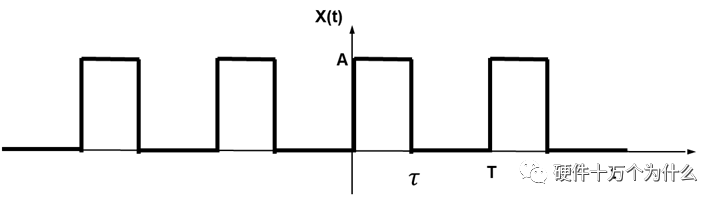
圖 14.4 周期為T的方波信號(hào)
周期為T的方波的三角函數(shù)的傅里葉級(jí)數(shù)可以表示為
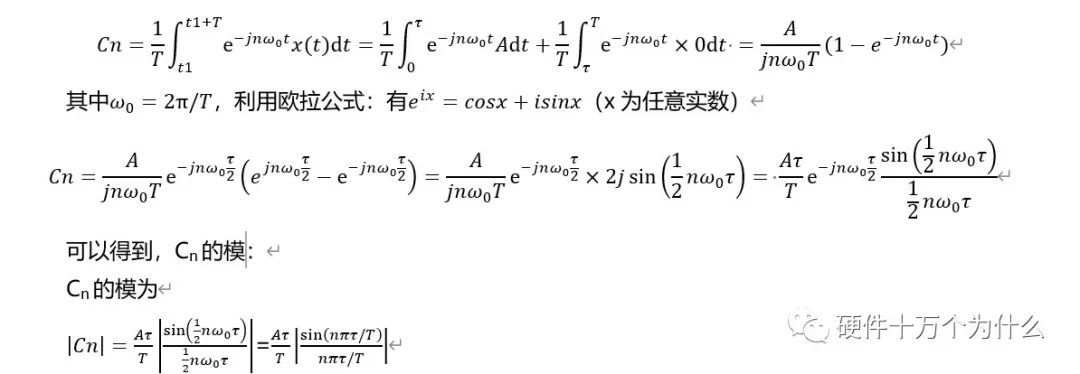
所以可以看到轉(zhuǎn)換到頻域,頻譜分量只存在在基頻f0=1/T的奇數(shù)倍(諧波)上。負(fù)數(shù)頻域在實(shí)際中不需要考慮,則Cn的頻譜特性如圖14.5所示。在圖中,標(biāo)注了頻譜的包絡(luò)線。
包絡(luò)線是一個(gè)信號(hào)在時(shí)域或頻域中振蕩的峰值點(diǎn)形成的曲線,表示了信號(hào)振蕩的上下界。包絡(luò)線通常用于描述一個(gè)信號(hào)的整體趨勢,而忽略了信號(hào)內(nèi)部的高頻振蕩。包絡(luò)線提供了一個(gè)有效的手段來捕捉信號(hào)振蕩的整體特征,而不受高頻細(xì)節(jié)的影響。
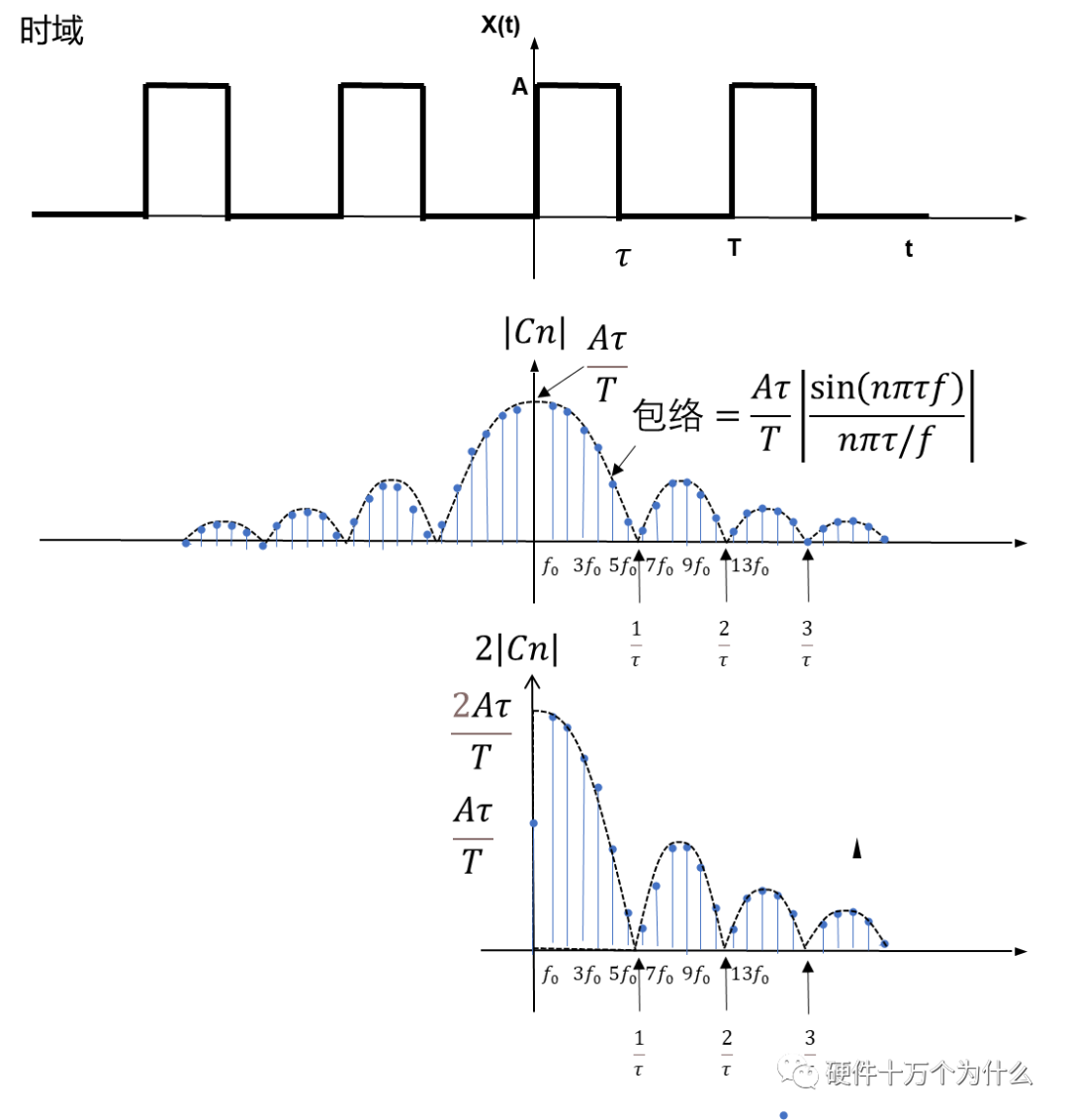
圖 14.5 方波的正頻率的單邊幅度頻譜
對(duì)于50%占空比的方波來說,只包含奇次諧波的分量,偶次諧波的分量為零。對(duì)于這個(gè)特點(diǎn),在我們實(shí)際的應(yīng)用中可以加以應(yīng)用。
以上分析的理想方波,上升時(shí)間和下降時(shí)間為零,但在實(shí)際應(yīng)用中沒有這么理想的方波,甚至我們希望通過減緩上升和下降時(shí)間來降低高頻的諧波分量。梯形周期脈沖波形如圖14.6所示。
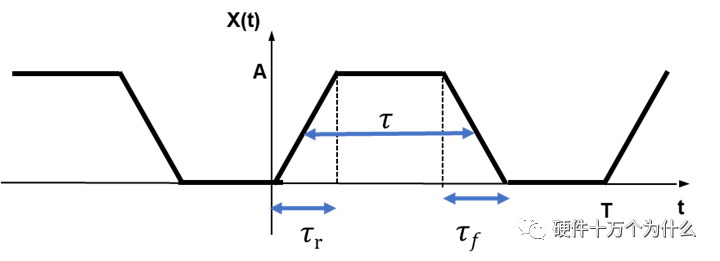
圖 14.6梯形周期脈沖波形
如圖的梯形波周期脈沖,原始的展開系數(shù)是
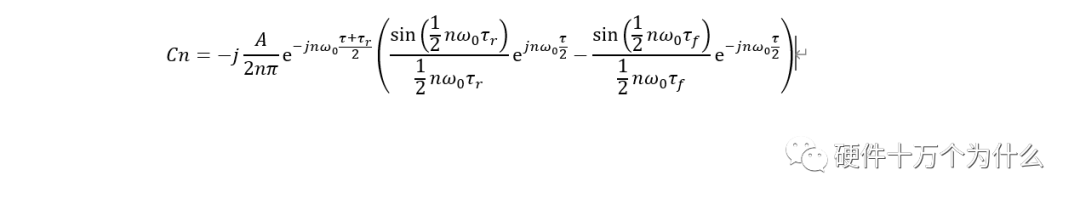
簡化分析,我們考慮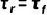 的特殊情況,可以進(jìn)一步合并,得到展開式的系數(shù)為,我們用τr來代替τf
的特殊情況,可以進(jìn)一步合并,得到展開式的系數(shù)為,我們用τr來代替τf
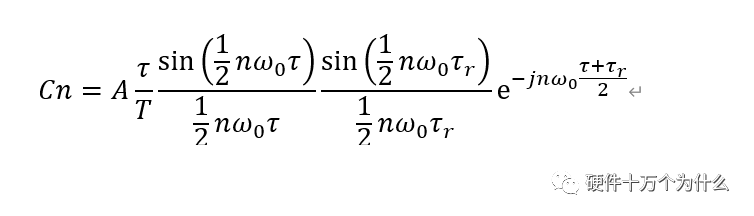
這個(gè)展開式對(duì)比方波的展開式,是包含兩項(xiàng)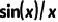 的乘積。在方波的分析中,雖然譜分量只存在在
的乘積。在方波的分析中,雖然譜分量只存在在
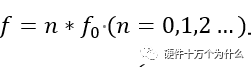
上,但是包絡(luò)具有的形式,它的邊界是確定的。

我們對(duì)方波和梯形波的展開系數(shù)做對(duì)數(shù)運(yùn)算,則兩種波形在頻譜上體現(xiàn)出梯形波的高頻分量明顯比方波更小,其高頻對(duì)外輻射也會(huì)更小。
方波的包絡(luò),如圖14.8(a)所示,形波的包絡(luò),如圖14.8(b)所示
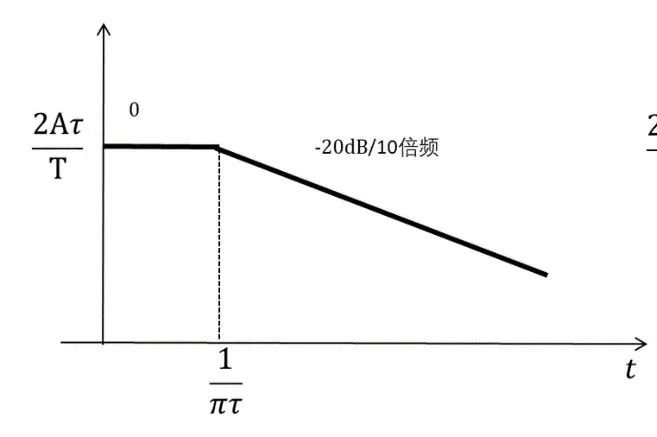
(a)方波
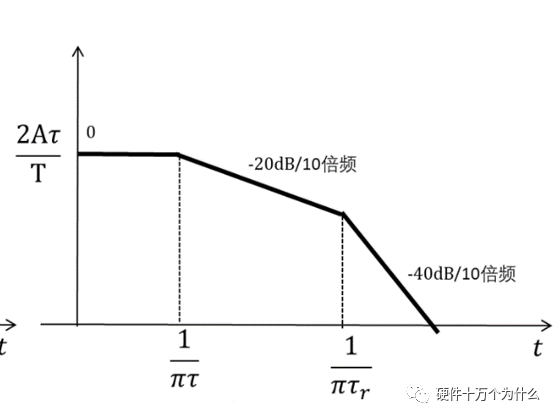
(b)梯形波
圖 14.8方波脈沖和梯形波的單邊譜邊界



評(píng)論