相量如何幫助我們理解帶通信號

使用相量，我們探索了在射頻通信系統中使用的模型中，如何將實值帶通信號表示為復基帶信號。

帶通信號和系統在通信系統中至關重要。有趣的是，實值帶通信號所攜帶的所有信息都包含在一個對應的復值基帶信號中。這種復基帶表示法對于理解無線電通信系統極為有幫助。

在本文中，我們將學習帶通信號的復基帶表示法。作為討論的一部分，我們還將探討交流電路中的相量分析概念。然而，在深入探討之前，讓我們先復習一下低通信號和帶通信號的定義，確保我們掌握了基礎知識。

低通信號和帶通信號

當信號的頻率內容或頻譜以零頻率為中心時，該信號被稱為低通信號。換句話說，低通信號具有一個明確的帶寬 B，并且對于 ∣f∣>B 的頻率，其頻譜含量可以忽略不計。

圖1展示了低通信號的實部和虛部。

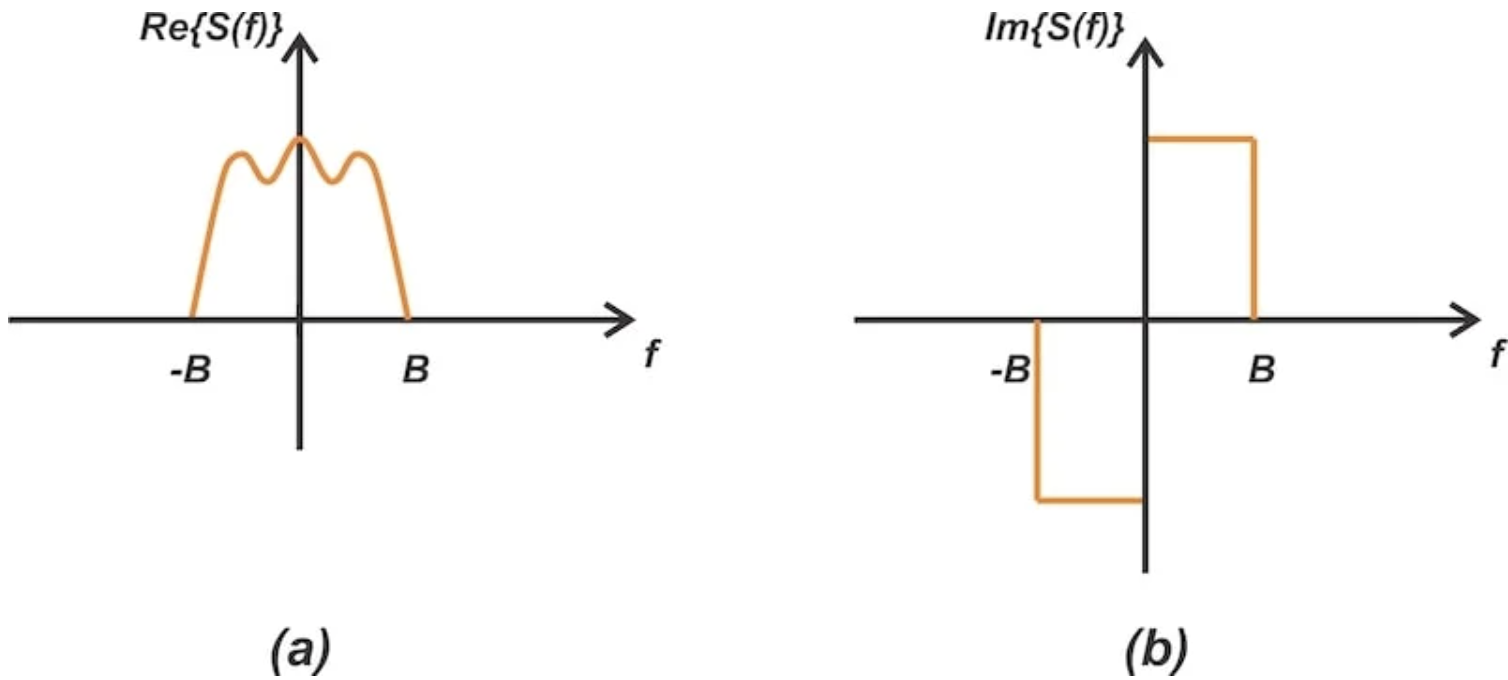
圖1. 帶寬為 B 的實值低通信號的實部（a）和虛部（b）。

請注意，如果 s(t) 是一個實值函數，其傅里葉變換 S(f) 將表現出共軛對稱性。這意味著 S(f) 的實部是一個偶函數，而虛部是一個奇函數。

另一方面，帶通信號的頻譜以一個頻率 fc 為中心，而該頻率遠大于信號帶寬 B。圖2展示了帶通信號的實部和虛部。

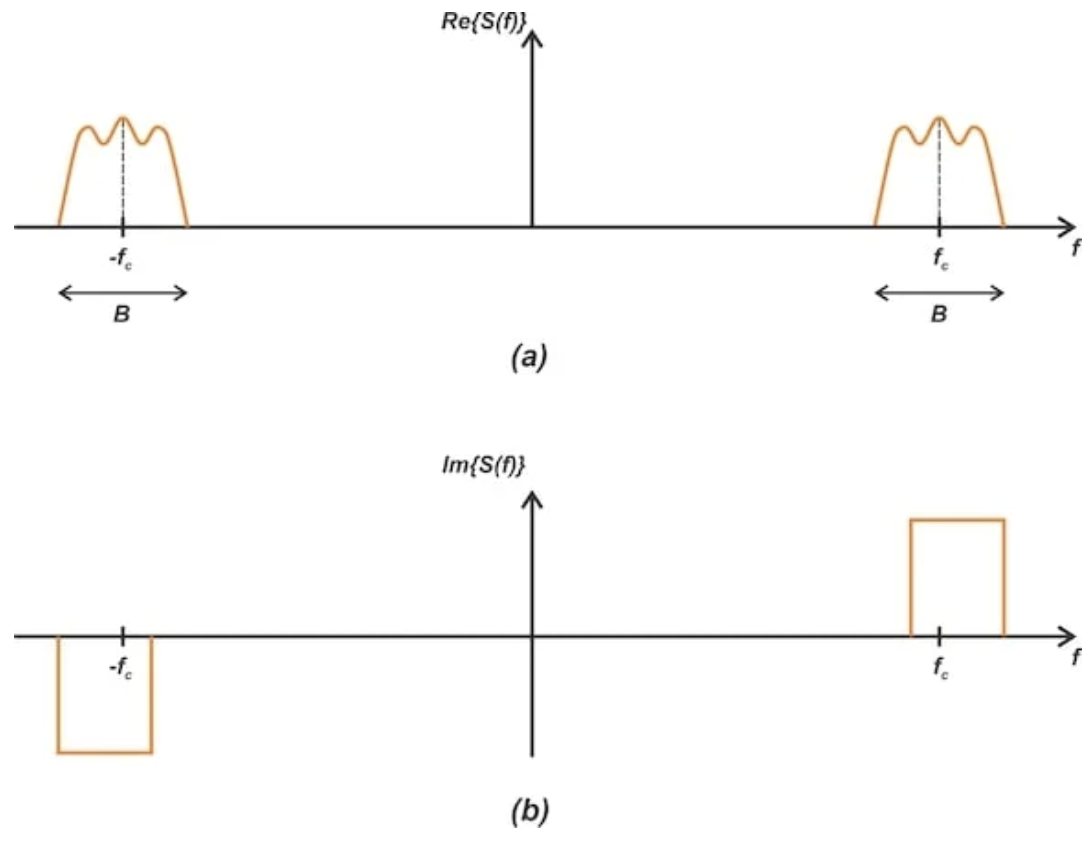
圖2. 中心頻率為 fc、帶寬為 B 的實值帶通信號的頻譜，分為實部（a）和虛部（b）。

與圖1中的基帶頻譜類似，圖2也因信號為實值而表現出共軛對稱性。

實信號的帶寬定義為信號中包含的所有正頻率分量的跨度。如果信號中最高的和最低的正頻率分別是 fmax 和 fmin，那么信號的帶寬為：

B=fmax?fmin

根據上述定義，單頻正弦波（頻率為 fc，幅度為 A）的帶寬為零。

s(t)=Acos(ωct+θ)

然而，如果 A 隨時間緩慢變化，那么我們得到的是一個具有非零帶寬的調幅（AM）波。

交流電路中的相量表示

相量是一個復數，用于表示正弦波形的幅度和相位角。在交流電路分析中，相量用于分析與頻率相關的效應。

例如，考慮公式2中所示的單頻正弦波。這個信號是一個復函數的實部：

s(t)=Re{[Aejθ]ejωct}

其中，操作符 Re{?} 表示大括號內量的實部。我們可以將大括號內的項表示為復平面上的一個向量，其幅度為 A，初始相位為 θ。如圖3所示，這個信號以角速度 ωc=2πfc 繞原點旋轉。

單頻正弦波的相量表示

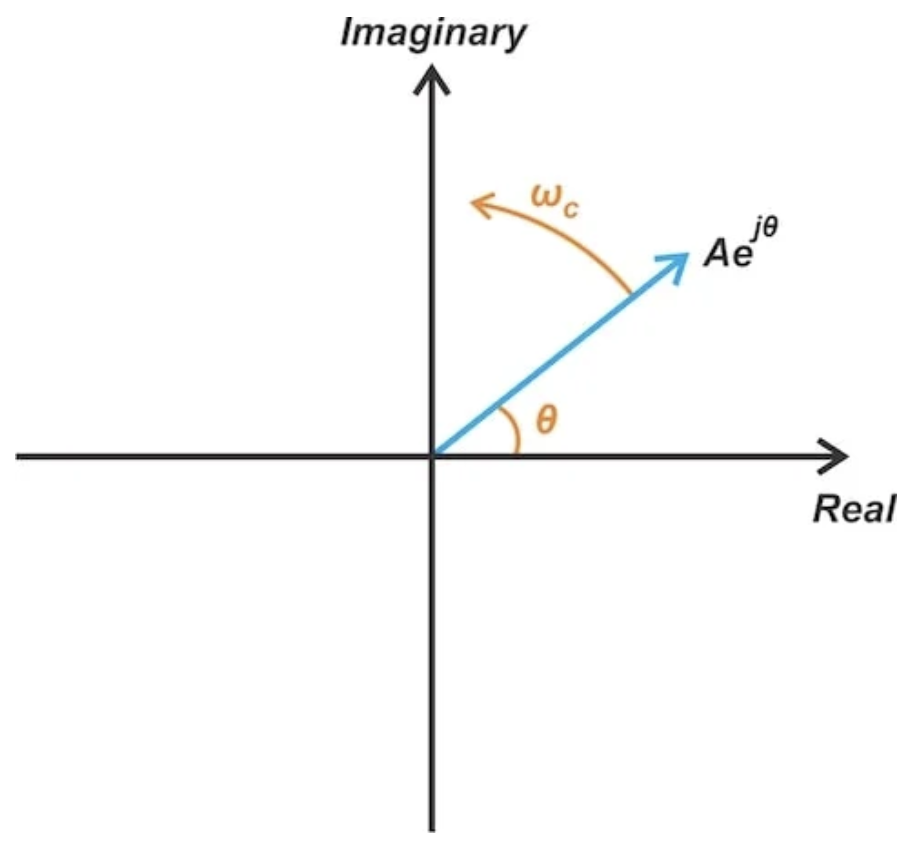
圖3. 單頻正弦波的相量表示。

該向量在實軸上的投影（即其實部）產生了公式2中所示的原始信號。角項 ωct 表示以每秒 fc 轉的速度進行穩定的逆時針旋轉。為了獲得信號的簡化表示，我們將暫時忽略這一項。

移除旋轉后，得到一個固定的向量，對應于公式3中括號內的項。這個與時間無關的項是與我們信號相關的相量。它由以下公式給出：

s~=Aejθ

要理解相量表示的意義，可以考慮一個由正弦輸入激勵的線性時不變（LTI）系統。如圖4所示，這種激勵在電路的所有節點上產生正弦信號。盡管所有這些信號的頻率相同，但它們的幅度和相位可能不同。

LTI電路產生的正弦信號可以用相量表示，這些相量具有不同的幅度和初始相位，但以相同的角速度旋轉

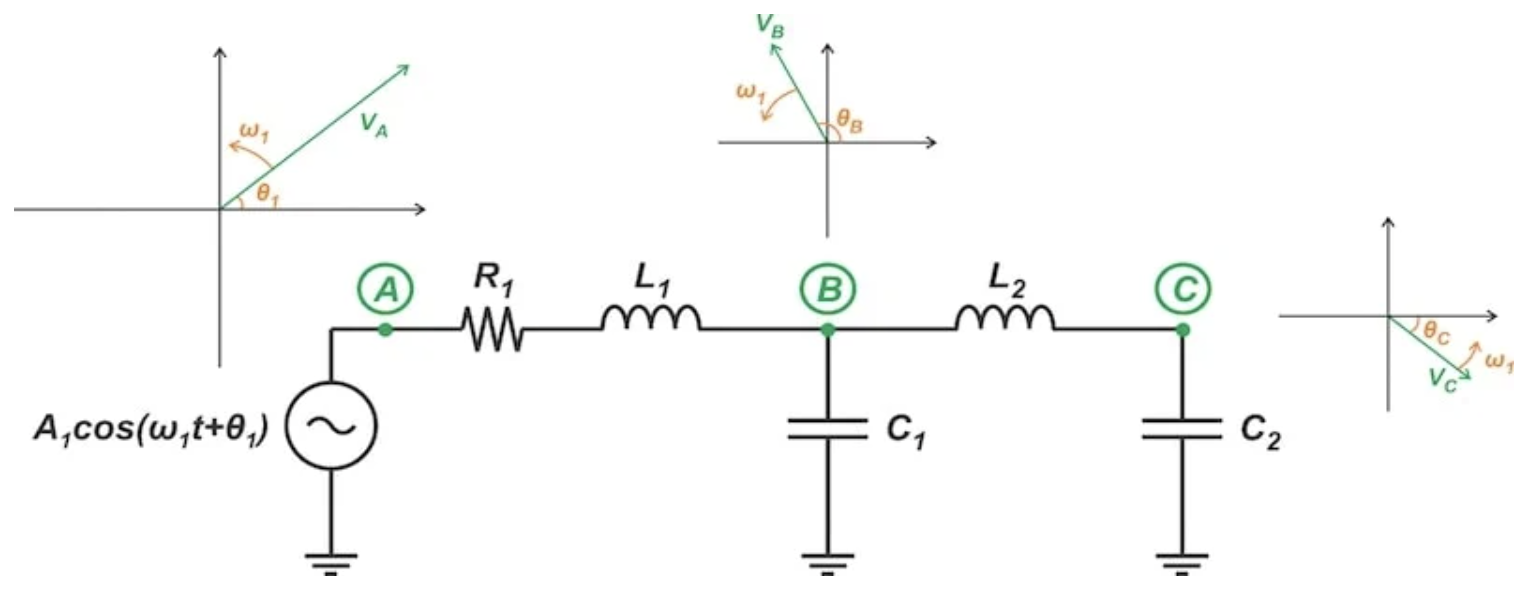
圖4. LTI電路產生的正弦信號可以用相量表示，這些相量具有不同的幅度和初始相位，但以相同的角速度旋轉。

由于所有這些向量以相同的角速度旋轉，它們之間的相位差不會隨時間改變。這些向量的幅度比也與時間無關。因此，我們可以在特定時刻凍結這些旋轉的向量。

從電壓和電流量中移除時間依賴性，使我們能夠將它們表示為復數值、與時間無關的數。這大大簡化了電路分析。一旦我們計算出某個電壓或電流量的向量，就可以重新引入旋轉部分，以確定該量的實際時域表達式。

簡而言之，相量消除了時間依賴性的復雜性，使描述電壓和電流量變得更加容易。通俗地說，你可以將相量視為單頻正弦波的低通或直流等效物。

推導調制帶通信號的低通信號等效形式

到目前為止，我們假設正弦波的幅度和相位是固定的。然而，類似的分析也可以應用于頻率為 fc 的正弦波，其幅度和相位隨時間緩慢變化。設以 fc 為中心的調制波定義為：

sRF(t)=A(t)cos(ωct+θ(t))

其中，A(t) 和 θ(t) 是時變信號的瞬時幅度和相位。上述公式可以改寫為：

sRF(t)=Re{[A(t)ejθ(t)]ejωct}

公式7將括號內的項分離出來：

sl(t)=A(t)ejθ(t)

這個項就是帶通信號的復基帶表示。上述公式也可以用笛卡爾形式表示：

sl(t)=si(t)+jsq(t)

其中，si(t) 和 sq(t) 是等效基帶信號 sl(t) 的實值同相分量和正交分量。這些分量由以下公式給出：

si(t)=A(t)cos(θ)和sq(t)=A(t)sin(θ)

由于帶通信號的同相分量和正交分量變化緩慢，我們知道它們都是低通信號。將 sl(t) 的笛卡爾形式代入公式6，我們可以用其同相分量和正交分量表示原始的射頻信號：

sRF(t)=si(t)cos(ωct)?sq(t)sin(ωct)

上述公式表明，帶通信號可以用兩個低通信號表示，即其同相分量和正交分量。

等效低通信號：可視化表示

帶通信號的復低通表示可以看作是一個時變相量，其起點位于 (sI?sQ) 復平面的原點。這在圖5中進行了說明。

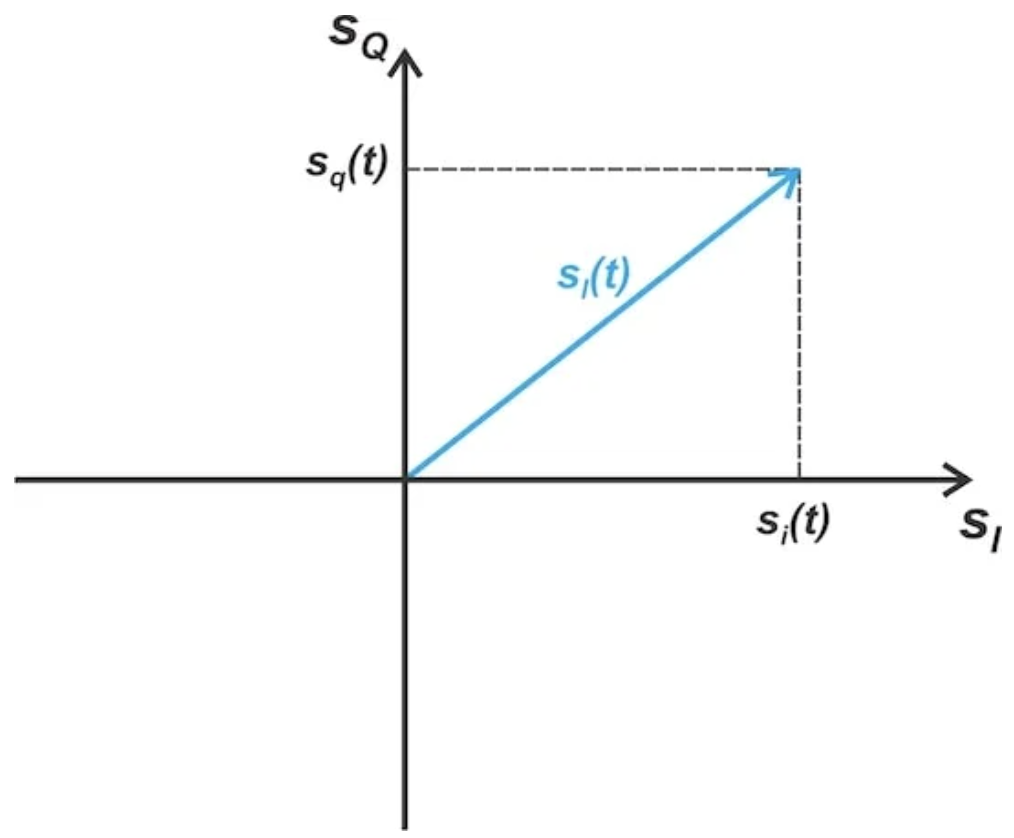
圖5. 等效基帶信號 sl(t) 作為 (sI?sQ) 平面上的時變相量。

由于同相分量和正交分量（分別為 si(t) 和 sq(t)）是時間的函數，因此相量的末端在 (sI?sQ) 平面上移動。

從公式6可以看出，等效基帶信號 sl(t) 乘以復指數 ejωct 產生帶通信號 sRF(t)。因此，向量 sl(t) 以及 (sI?sQ) 平面以角速度 ωc=2πfc 旋轉。

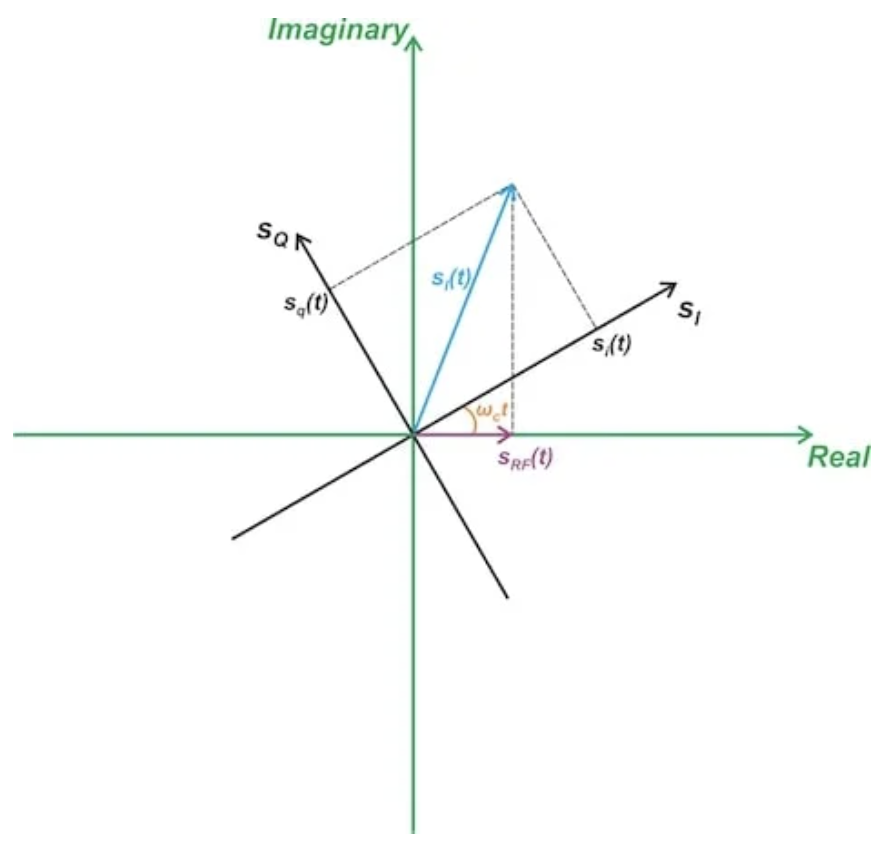
圖6. 包含旋轉部分的復平面上的時變相量。

原始的帶通信號 sRF(t) 是這個時變相量在表示實軸的固定線上的投影。

重建帶通信號

公式10立即告訴我們如何從同相分量和正交分量重建帶通信號。從低通到帶通的轉換電路如圖7所示。

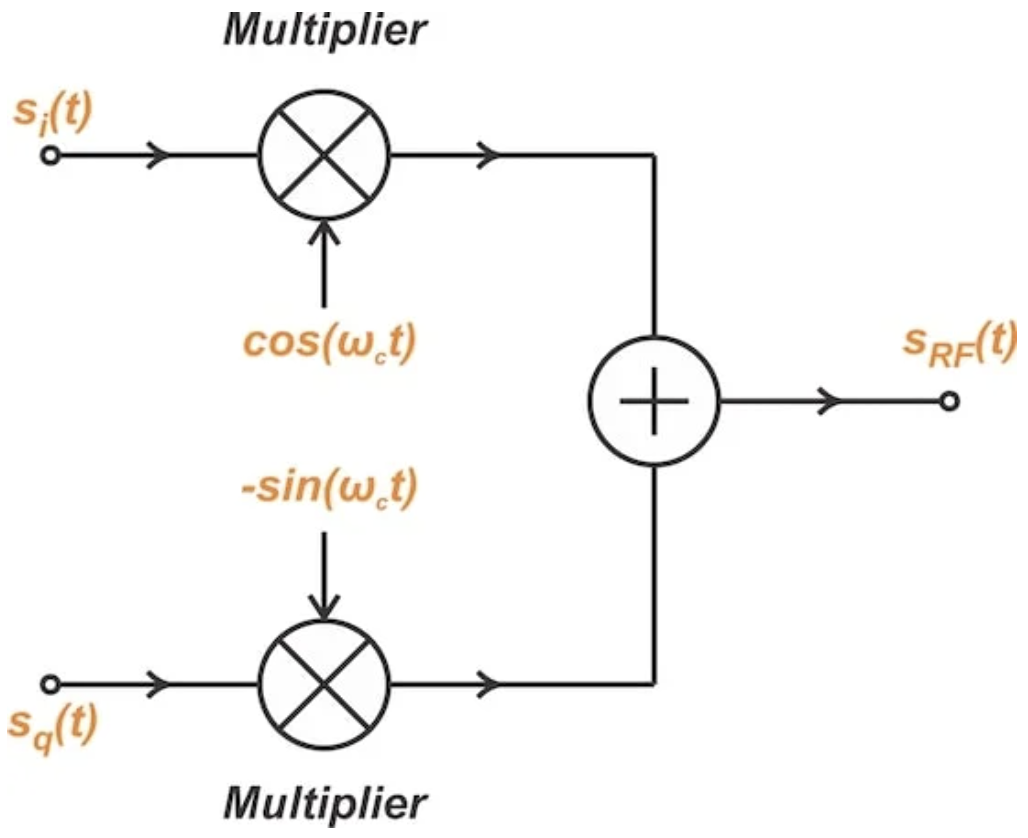
圖7. 從低通同相和正交信號生成帶通信號的框圖。

接下來，我們需要從帶通信號中確定等效基帶信號。我們首先將 sRF(t) 乘以 2cos(ωct)：

sRF(t)×2cos(ωct)=A(t)cos(ωct+θ(t))×2cos(ωct) =A(t)[cos(2ωct+θ(t))+cos(θ(t))]

如果我們濾除兩倍載波頻率的信號分量，我們得到：

Lowpass[sRF(t)×2cos(ωct)]=A(t)cos(θ(t))=si(t)

類似地，將 sRF(t) 乘以 ?2sin(ωct) 產生：

sRF(t)×(?2sin(ωct))=A(t)cos(ωct+θ(t))×(?2sin(ωct)) =?A(t)[sin(2ωct+θ(t))?sin(θ(t))]

應用適當的低通濾波器可以消除兩倍載波頻率的信號分量，得到：

Lowpass[sRF(t)×(?2sin(ωct))]=A(t)sin(θ(t))=sq(t)

圖8展示了如何使用一對乘法器和一對低通濾波器實現公式12和公式14。

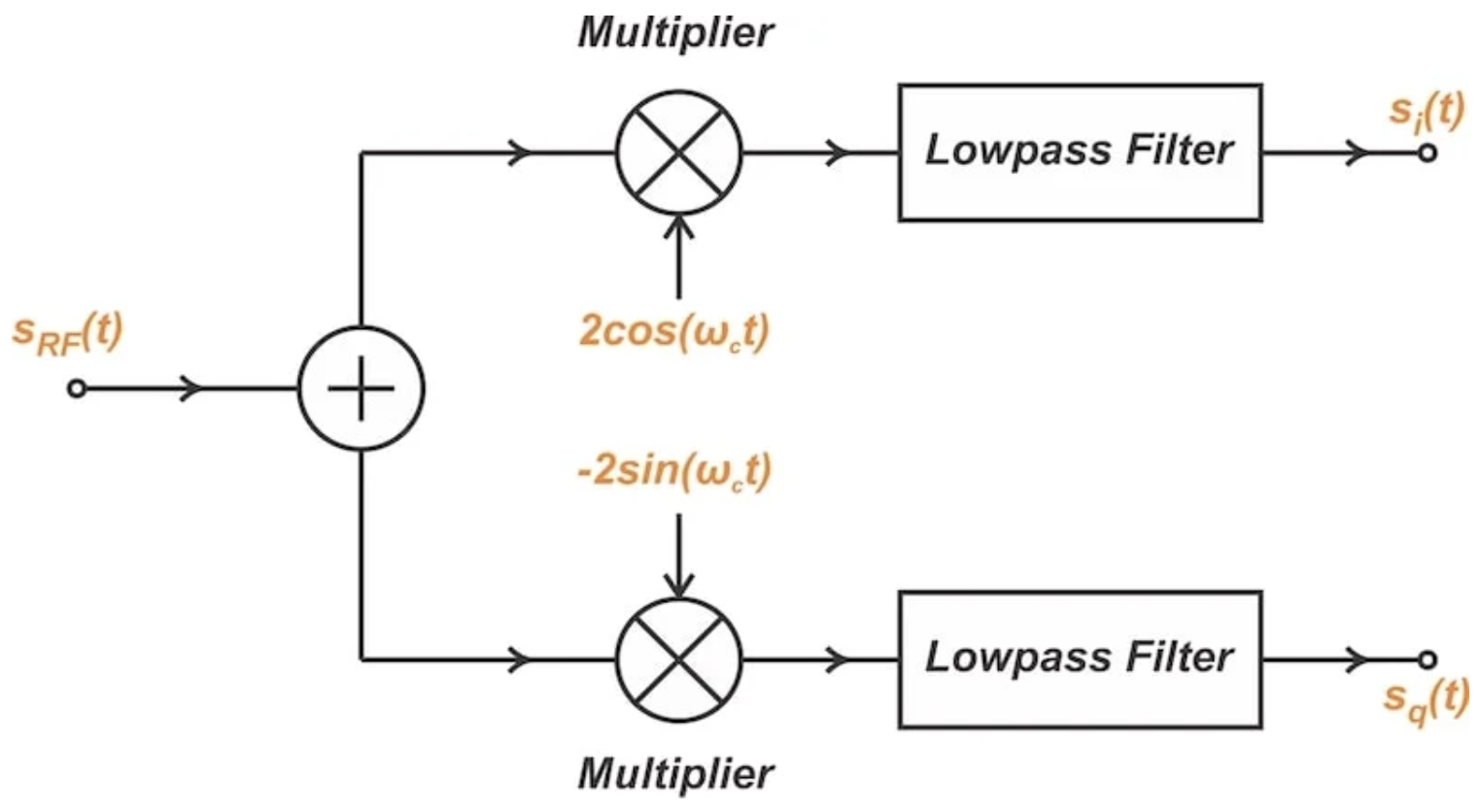
圖8. 從帶通信號生成低通同相和正交信號的框圖。

總結

實值帶通信號中的所有信息都包含在一個對應的復值基帶信號中。在本文中，我們學習了如何推導帶通信號的低通信號等效形式，反之亦然。

值得注意的是，擴展這一討論可以讓我們用復低通濾波器來表示帶通濾波器。為帶通信號和濾波器都建立低通模型具有極其重要的實際意義。例如，現代通信收發器應用這些模型來數字處理復基帶信號，從而減少了對帶通信號的模擬處理需求。

圖7和圖8中所示的電路對于理解線性調制方案至關重要，無論它們是模擬的還是數字的。在下一篇文章中，我們將看到Weaver調制器如何利用這些電路生成單邊帶調幅信號。