靜電槍電路模型的建立及驗證

0   引言

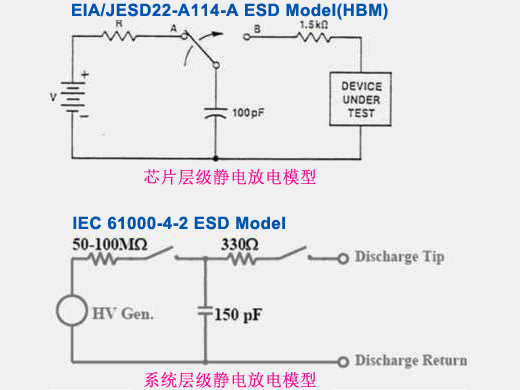
ESD（靜電放電）是由于金屬和非金屬幾何結構上電荷的積累，通常是摩擦起電。這種帶電體直接或間接的相互作用是ESD放電發生的主要原因。ESD脈沖的泄放，使產品的軟硬2種失效都有可能發生。所以電子產品對ESD的監測和防護是十分有必要的。系統級ESD測試的主要測試標準是國際電工委員會規定的IEC 61000-4-2^[1]。為了確保電子產品在遭受ESD脈沖時和ESD脈沖過后都能夠繼續正常工作，需要實施系統級ESD測試。在系統級ESD測試過程中，我們用ESD發生器（靜電槍）來模擬ESD放電場景，但是頻繁地進行實際系統級防靜電測試是昂貴和耗時的過程，因此有必要尋求1種有效的方法來分析和預測設備的靜電防護能力。

作者簡介：蘆俊，男，碩士生。郵箱：junlu.xt@foxmail.com。

1   IEC61000-4-2標準

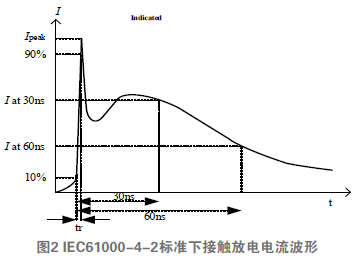
在IEC61000-4-2標準中，靜電槍電路如圖1所示，已充電的150 pF電容器通過330 Ω電阻放電，從而產生如圖2所示的電流波形，該波形中有2個峰值。 根據測試電壓，從(2~8) kV分為4個等級，每個等級相差2 kV，不同等級下對應的特性參數也不同。第1個峰值電流為3.75 kV/A，誤差不得超過15％。30 ns的電流為2 kV/A，誤差不大于30％，60 ns的電流為1 kV/A，誤差小于30％。波形的上升時間占第一峰值電流的10％至90％，通常為0.8 ns，誤差不能超過25％。然而這個誤差范圍相對較大，可能引起仿真結果的不準確。現存的電路模型精確度雖然有所提高，但與標準值還是有些差距^[2-3]。本文對電路模型進行優化后，在Cadence下進行模型的搭建與仿真，其輸出波形的特征參數與標準值接近一致。

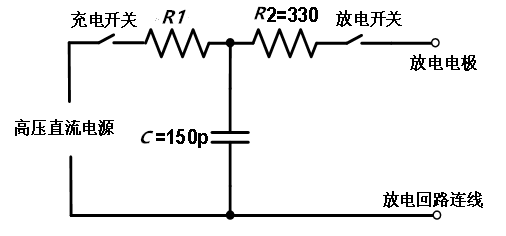
圖1 IEC61000-4-2標準下接觸放電電路簡圖

2   接觸放電電路模型

2.1 數值計算

我國學者盛松林曾提出接觸放電波形可以看做一大一小2個波組合而成，并且用數值表達式擬合出接觸放電電流波形，但他的模型是基于度量的，沒有電路特性^[4]。在電路上可以用2個不同的電容放電來形成這樣的波，電路結構設計如圖3所示。圖4是靜電槍電路的s域模型，設a點電壓為Y（s），則可以列出a點的節點方程^[5]：

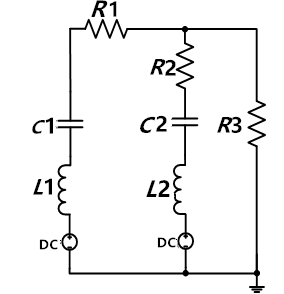
圖3 接觸放電模型電路原理圖

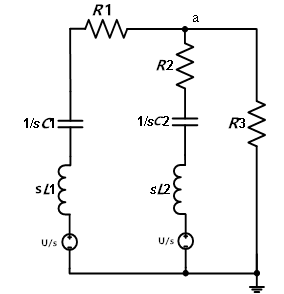
圖4 s域電路模型

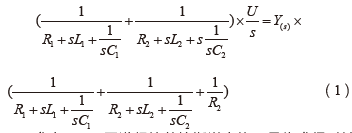
求出I_（s），再進行拉普拉斯逆變換，最終求得時域中的電流I_（t）^[6]。

通過計算發現，第1峰值的大小主要由R2、C2、L2決定，它會隨著C2的增加，R2的減小而變大；第2峰值主要由R1、C1、L1決定，它會隨著C1的增加，R1的減小而變大。R3為待測器件的阻值，一般是2 Ω。最終元件參數值如表1所示。

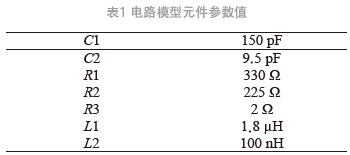
圖5是電壓為2 kV下的數值計算波形與實測波形的對比圖（紅色線是MATLAB下數值計算曲線，藍色線是實測曲線），可以看出兩者的吻合度是比較好的。波形的特征參數值如表2所示。

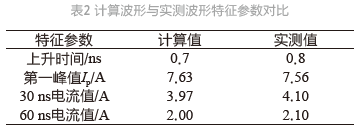
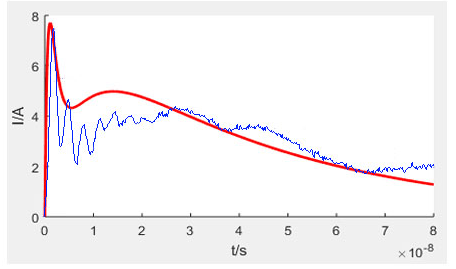
圖5 2 kV下接觸放電模型的數值計算與實測對比圖

2.2 電路仿真

為了進一步驗證模型的準確性，在Cadence環境下搭建了電路并進行了仿真，仿真結果如圖6所示。可以看出各等級下波形的特征參數都符合IEC61000-4-2標準且具有較高的精確度。其中，第1峰值電流誤差在2.8%以內，30 ns電流值誤差在3.1%以內，60 ns電流值誤差在2.5%以內。可見，此模型具有很好的精確性與穩定性，很適合用于接觸放電仿真測試。

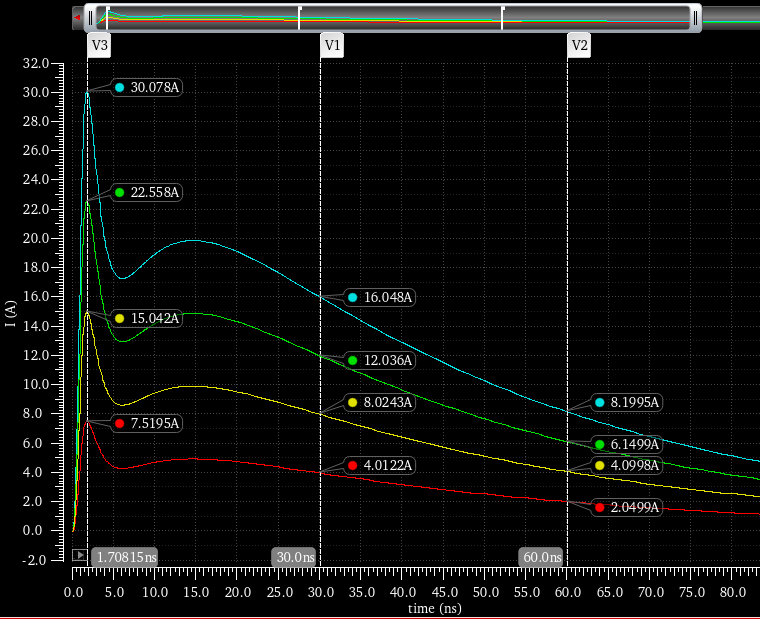
圖6 Cadence下接觸放電仿真波形圖

3   HBM電路模型

為了擴展模型的實用性，把接觸放電模型改成了HBM模型。圖7為靜電槍的HBM模型，它與接觸放電模式的不同點在于：原電路中R1的阻值由330 Ω變成1.5 kΩ，C1的電容值由150 pF變為100 pF。2 kV下模型產生的放電電流波形如圖8所示，其中紅色線是Cadence下仿真曲線，藍色線是實測曲線，可以看出兩者的吻合度也是很好的。改進后的模型可用于靜電仿真測試中的HBM測試。

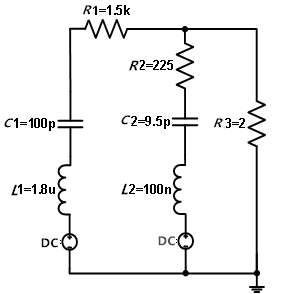
圖7 HBM模型電路原理圖

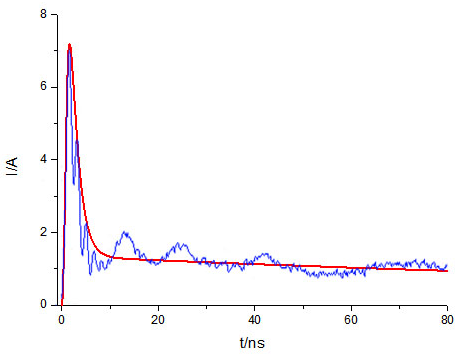
圖8 2 kV下HBM模型的仿真與實測對比圖

4   結論

本文提出了一種新的靜電發生器電路模型，該模型在Cadence中建立并驗證。優點是：①模型產生的波形很穩定且與實測波形的吻合度較好；②適用于2種測試模式，接觸放電測試和HBM測試。其中，接觸放電的仿真結果與IEC61000-4-2標準非常吻合。第1峰值電流誤差在2.8%以內，30 ns電流值誤差在3.1%以內，60 ns電流值誤差在2.5%以內。此外，HBM模型的仿真結果與實測波形的吻合性也很好，從而證實了新模型系統行為的準確性。該電路模型為靜電放電仿真提供了1個新的激勵源。

參考文獻：

[1] Electromagnetic Compatibility (EMC) Part 4-2: Testingand Measurement Techniques-Section 2: ElectrostacticDischarge (ESD) Immunity Test, TEC-EN 61000-4-2,2008.

[2] 田巍,石磊.靜電放電發生器模型的研究及應用[J].科技廣場,2011(07):82-84.

[3] MERTENS R,KUNZ H,SALMAN A,et al.A flexiblesimulation model for system level ESD stresses with application to ESD design and troubleshooting[C],Electrical Overstress/Electrostatic Discharge Symposium (EOS/ESD), 2012 34th. IEEE, 2012.

[4] 盛松林,畢增軍,田明宏,等.一個新的IEC61000-4-2標準ESD電流解析表達式[J].強激光與粒子束(5):464-466.

[5] 邱關源.電路.第5版[M].北京:高等教育出版社,2006.

[6] TANAKA H,FUJIWARA O,YAMANAKAY.A Circuit Approach to Simulate DischargeCurrent Injected in Contact with an ESDgu n [ C ]，I n t e r n a t i o n a l S y m p o s i u m o nElectromagnetic Compatibility.

（本文來源于《電子產品世界》雜志2020年8月期）