蟻群算法在一種物聯網醫療箱系統上的調度研究與應用
盧嘉軒,李 晉,周 延
本文引用地址:http://www.104case.com/article/201907/402149.htm(上海大學 機電工程與自動化學院 工程訓練國家級教學實驗示范中心,上海 200444)
摘要:針對一種物聯網醫療箱系統,提出了一套使用機器學習和蟻群算法的藥物調度方法。該方法使用閾值劃分的方式,對取藥記錄建立了嶺回歸、隨機森林回歸和神經網絡的混合模型,以預測不同醫療箱中各類藥物的需求量。之后,根據硬件檢測的藥物實際數量,計算出各藥物的偏差值,在將調度問題轉換為旅行商問題以后,分別使用基本蟻群算法和最大最小蟻群算法對調度問題進行了求解和對比。實驗表明,該方法能較好地預測藥物的需求量,規劃出一條合理的藥物調度路徑,為物聯網醫療箱系統的藥物調度提供了一種數據驅動的解決方案。
0 引言
隨著智能醫療概念的興起,自動售藥機和自助醫療箱在英美等國得到了廣泛推廣,在我國也逐漸普及。然而,傳統自動售藥機在日常運營中需要進行人為的藥物檢查和補給,在藥物的調度上也沒有一套較為合適的方案。除此之外,由于地理限制和宣傳力度欠佳,售藥機常常無人問津,使用率較低。為此,一種基于物聯網的校園醫療箱系統應運而生,該系統由若干放置在學校不同位置的聯網的醫療箱所組成,可以在短時間內為師生突發的創傷提供及時有效的救治藥物及必要的救援器具。該藥物箱系統已在某高校進行了試運營,用戶可以通過微信小程序的終端查看附近的藥物箱位置和藥物余量,所有取藥記錄也將上傳至服務器,保存在數據庫中。
本文基于該新型物聯網醫療箱系統,提出了一種根據歷史取藥記錄和藥物余量進行調度的通用方法。該方法分為藥物需求量預測和藥物調度路徑規劃兩大步驟。在需求量預測的實驗中,針對歷史取藥記錄,建立了嶺回歸、隨機森林回歸和神經網絡的混合模型,以預測各醫療箱中藥物的需求量。在調度路徑規劃的實驗中,將預測的藥物需求量與實際數量進行比較,將偏差量定義為藥物實際數量與預測需求量之差。該方法將藥物的調度問題轉化為多個供應商和多個需求者之間的特殊旅行商問題(Traveling Salesman Problem,TSP),并分別使用基本蟻群算法(Ant System,AS) [2] 和最大-最小蟻群算法(Max-Min Ant System,MMAS) [2-5] 進行了求解和對比。該方法能為新型物聯網醫療箱系統的藥物分配與調度提供解決方案,有效降低日常運營成本。
1 需求量預測
由于物聯網醫療箱具有藥物檢測、數據上傳的特點,因此所有的取藥記錄和藥物余量都會保存在云服務器中,這也為模型的建立提供了必要的數據支持。對于某類存放于醫療箱中的藥品,影響其需求量的因素可以大致概括為3類:所處時間,醫療箱地理位置和藥物自身特性。針對醫療箱系統而言,取藥記錄間接地反映了特定時間、特定地理位置上各類藥品的需求量。為此,可以通過歷史取藥記錄的數據,建立上述3類因素到藥品需求量的映射關系。
具體地,所處時間包括歷史取藥日期以及對應的月份和星期;地理位置包括醫療箱所處的經緯度數值和地理畫像,如地圖興趣點(Point of Interest,POI)密度、是否位于宿舍、食堂、運動場、體育館、實驗室等特殊場所等;藥物自身特性,包括藥物所屬的類別以及由行業認可的藥物評審數據庫提供的藥物評分等。在獲取并整合上述數據以后,即可以使用機器學習算法構建藥品需求量與各因素之間的模型,即通過輸入上述特征來預測特定日期、特定地理位置下某藥品的日需求量或多日需求量。本文使用的模型包括嶺回歸、隨機森林回歸和神經網絡。
嶺回歸(Ridge Regression) [9] 是線性回歸問題中一種改良的最小二乘估計法,即在最小二乘估計法的損失函數中加上L2正則項,通過放棄最小二乘法的無偏性為代價以獲得更合適的回歸系數,防止過擬合。嶺回歸由于可供訓練的參數較少,在數據量不太大、線性可分性強的問題上表現較優。
隨機森林回歸(Random Forest Regression) [9-11]是一種針對分類與回歸樹(CART,Classification AndRegression Tree)進行集成的方法,通過取每棵CART回歸樹葉子結點的均值來得到預測值。相比于使用最小化基尼系數來選擇特征的CART樹,隨機森林往往擁有更強的泛化能力,在處理回歸問題上也具有較好的通用性。
神經網絡(Neural Networks,NNs) [9,10,12] 也稱人工神經網絡,是一種模仿大腦神經突觸聯接的結構進行信息處理的數學模型。該網絡使用大量基本神經元進行計算,并能通過反饋機制來優化網絡參數,擁有學習的能力。深度神經網絡在擁有大規模訓練數據的任務上表現突出,但由于可供訓練的參數數量龐大,在數據量過小的任務中可能遜于普通的機器學習算法。
由于不同醫療箱中的藥品索取量和需求量可能不在同一個量級上,使用單一模型進行預測并不合適。為此,本文采用閾值劃分的方式,針對數據量小于某個閾值的藥品,采用簡單的嶺回歸模型進行預測;而針對數據量大于該閾值的藥品,采用較為復雜的隨機森林回歸和神經網絡共同進行預測,并把這兩個模型輸出的均值作為最終的預測值。實驗表明,這種方式能獲得比單一模型更高的準確率。
2 調度路徑規劃
2.1 問題描述與建模
物聯網醫療箱的藥品調度是醫療箱系統日常運營中的關鍵問題,主要包括數量和路徑兩大難題,即需要向各醫療箱投放多少藥品以及如何規劃投放和調度的路徑。在傳統的自動售藥機模式中,運營方需要事先預估各售藥機的藥品需求規模,并人為地對藥品的余量進行檢查和補充,是一種基于經驗的方法。而在數據驅動的物聯網醫療箱系統之下,由于所有的藥品需求量可以由已訓練的網絡計算得出,因此可以將預測值與硬件檢測的實際藥品數量進行比對,確定各類藥物的供需關系。
為此,本文假設醫療箱中的藥品數量需要滿足該藥品N日內的需求,并定義醫療箱k中藥品的偏差量β k,i 為當前該藥品的實際數量與該藥品N日需求總量之差,即

其中,r k,i 為醫療箱k中當前藥品i的實際數量,可以由硬件檢測并上傳數據庫獲取得到;p k,i 為預測的醫療箱k中藥品i的日平均需求量。若β k,i 大于0,表明該醫療箱中的這類藥品處于供大于求的狀態,可以調出;若β k,i 小于0,則表明該藥品處于緊缺狀態,希望調入。由此,醫療箱系統的藥物調度問題即可轉化為一個特殊的旅行商問題(TSP),即派一輛小車從特定站點出發,訪問各醫療箱和藥房、醫院、倉庫等藥物供應站點,尋找出總路程最短的Hamilton圈,并在這個過程中完成藥物的調度。
設G=(C,L)是一個有向圖,其中 C ={ c 1 , c 2 ,?,c m }為m個醫療箱或供應站點的集合,L={l ij |c i ,c j ∈C為集合C中元素兩兩連線構成的邊集, d i,j ( i,j =1,2,..., m )為醫療箱 i 和j 之間 l ij 的行車距離,可以通過調用地圖軟件API接口獲取其數值。在傳統的TSP問題中,所有的站點是沒有區分性的,即可以任意選擇站點作為路徑的延續。而在本問題中,由于需要進行藥物的調度,因此對于候選站點k的選擇有如下的約束條件:
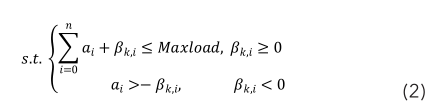
其中,a i 為當前貨車上已有藥物i的數量,β k,i 為醫療箱k中藥品i的偏差量,Maxload為貨車的負載量上限。當結點k的偏差量大于等于0,即該藥品供大于求時,需要將其移上貨車,要求移上貨車后藥品總數量不超過貨車的最大負載量;當結點k的偏差量小于0,即該藥品供不應求時,要求貨車上有足夠多的該類藥物以補給醫療箱。
如果一個醫療箱中所有藥品都滿足上述約束條件,且該站點還未訪問,則稱該站點為該時刻的有效候選站點。
調度路徑搜索的目標就是不斷選擇有效候選站點,直到所有站點都已被訪問。
2.2 基本蟻群算法
蟻群算法(Ant System,AS)是一種模擬進化的算法,由意大利學者多里科(Marco Dorigo)于1991年提出,通過模擬螞蟻在覓食過程中釋放信息素優化路徑的行為,構建了一套人工的螞蟻系統。蟻群算法在求解TSP問題中得到了廣泛應用,也因此作為本文醫療箱藥物調度問題的基本求解算法。
在算法的開始,將q只螞蟻隨機地置于m個醫療箱站點上。對于每只螞蟻,都擁有一張屬于自己的禁忌表tabu k ,用來表示螞蟻k已經訪問過的醫療箱站點。在本問題中,由于候選站點的約束條件限制,因此需要額外設置一張無效候選站點表invalid k 作為不滿足公式(2)的候選站點的集合。
在t時刻,在醫療箱 i 處的螞蟻 k 需要根據該時刻的有效候選站點集J k (i),依據某一概率函數選擇下一個站點j。其中,有效候選站點集J k (i)為去除了禁忌表中元素和無效候選站點表invalid k 中所有元素的站點集合,即
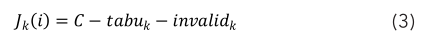
螞蟻從站點轉移到站點的轉移概率定義為:
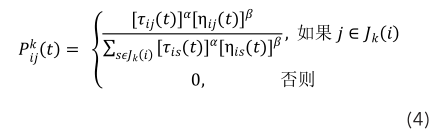
否則其中, α 為信息啟發式因子,表示軌跡的相對重要性;β 為期望啟發式因子,表示能見度的相對重要性; η ij (t)是啟發函數,表示螞蟻 k 從站點 i 轉移到站點 j 的期望程度,這里取站點 i 和站點 j 實際行車距離的倒數,即

式中,站點 i 到站點 j 實際行車距離 d i,j 越小,則 η ij (t) 越大,因此 η ij (t) 可以表示為螞蟻從站點i轉移到站點j的期望程度。
在算法的起始階段,所有邊上的信息素量是相等的,即 τ ij (0)=C ( C 為常數)。當所有螞蟻都尋找到一條Hamilton回路后,各路徑的信息素量根據下式來更新:
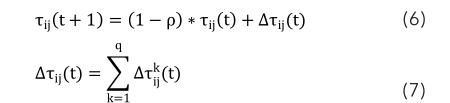
其中, ρ 為信息素的蒸發系數, Δτ ij (t) 為本次迭代中邊 l ij上信息素的增量, Δ 為螞蟻 k 在本次迭代中留在邊l ij 上的信息素。在Ant-Cycle模型中,定義為:

式中, Q 為正常數,表示信息素的強度; L k 為螞蟻 k 在本次迭代中所經路徑的總長度。在每一輪迭代中,所有的螞蟻都去尋找一條Hamilton回路,并更新信息素,開始下一輪迭代。當迭代輪次達到最大進化次數時,算法結束,當前的最優Hamilton回路即為算法尋找到的最優調度路徑。
2.3 最大最小蟻群算法
基本蟻群算法提供了一種求解TSP問題的方案,但是其存在收斂速度較慢、易陷于局部最優的缺點。為此,Stutzle和Hoos提出了最大-最小螞蟻系統(Max-MinAnt System, MMAS)。相較于基本蟻群算法(AS),最大最小蟻群算法做了如下改進:
1)采用全局信息素更新,即在每一輪迭代結束后,僅更新本輪或全局最優解路徑上的信息素,以加強最優解的影響力,即將式(6)和(7)修改為:
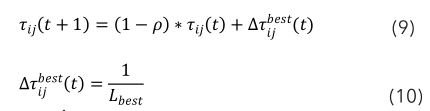
其中,為本次迭代中最優路徑或全局最優路徑上信息素的增量,其值等于最優路徑的總長度 L best 的倒數。
2) 限制每條邊上的信息素在固定范圍[τ min ,τ max ]內,避免某條路徑上的信息素量遠大于其他路徑,造成算法過早收斂于局部最優解。
3)將初始時刻各條邊上的信息素量τ ij (0)設為τ max ,而不再是一任意的常數 C ,使算法在初始階段能擁有較高的隨機性,以提高發現全局最優解的概率。
3 實驗與結果分析
3.1 數據描述與預處理
本文的實驗數據來源于正在上海大學寶山校區試運營的醫療箱系統后臺,由于用戶需要使用微信小程序進行取藥,因而所有的取藥記錄都會保存在云服務器的MySQL數據庫中。取藥記錄包括取藥時間、醫療箱編號、藥物編號、藥物名稱等字段。本實驗使用Python訪問數據庫,讀取取藥記錄,并進行了數據的處理和整合,統計出了各醫療箱中各類藥物的平均日索取量。
針對取藥日期,將其轉化為項目開始運營到該日期的偏差天數,并加入該日期所對應的月份和星期作為模型的輸入字段;針對醫療箱位置,調用經緯度轉換函數將其編碼為可以用單個字段反映地理坐標的GeoHash格式 [13] ;針對醫療箱所在位置的特殊地理類型,如運動場、游泳館、實驗室、宿舍等,分別進行One-Hot編碼將其轉化為8個字段;針對藥物評分,通過API接口調用了全球藥物評審數據庫SERMO的相關評分數據。
為了更好地刻畫醫療箱的地理畫像,本實驗調用Google地圖接口分類統計了各醫療箱地理坐標附近的興趣點(POI)數量,包括餐飲類數量、公司企業類數量、購物商場類數量、交通設施類數量、道路地名類數量等。最后,將所有上述字段和對應的日索取量進行歸一化處理以消除量綱的影響。
3.2 需求量預測
本文假設歷史取藥記錄中的索取量間接地反映了特定醫療箱中該藥品的需求量,希望能夠構建一個由上述特征到藥物日平均需求量的映射關系。由于經預處理后的特征向量維數過高,本文使用主成分分析(Principalcomponents analysis,PCA)的方法對特征向量進行降維,并以8:2的比例劃分訓練集和測試集。


本實驗中,設定劃分閾值為 w ,即訓練集中數據條目少于的 w 藥品,使用嶺回歸進行建模,否則分別使用隨機森林回歸和神經網絡進行建模與預測。其中,嶺回歸和隨機森林由Python的機器學習庫Scikit-learn實現,隨機森林的子模型數n_estimators設為30;神經網絡使用Keras框架下的反向傳播算法(BP)進行實現,包括輸入層和輸出層共6層,每層的神經元個數分別為[31,100,50,30,10,1],激活函數使用ReLU函數,梯度優化使用Adam算法,本文使用均方根誤差(RMSE)來衡量模型的預測精度,即

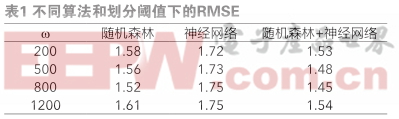
式中, p gt,i 為真實的藥品平均日需求量, p model,i 為模型預測出的藥品日需求量。本實驗根據上述參數設置,調整劃分閾值w,針對數據量小于w的藥品統一使用嶺回歸進行建模,針對其他藥品分別使用隨機森林回歸、神經網絡、隨機森林與神經網絡取均值的算法進行了實驗,計算出了所有藥品的整體均方根誤差,如表1所示。
3.3蟻群算法路徑調度
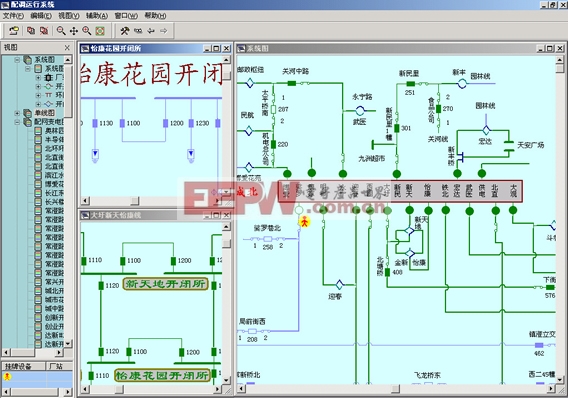
在得到各醫療箱中各類藥品的日需求量,即可根據硬件檢測的實際數量計算出各類藥品的偏差值。實驗中假設 N =7,n =5,即每個藥物箱中共有5件藥品,要求調度結束后每件藥品能夠滿足7日的需求量。由于當前物聯網醫療箱僅在上海大學寶山校區試點運營,數量不多,因此本文模擬了50個醫療箱和藥品提供商的站點,以檢驗蟻群算法的調度效果。本實驗使用Python的圖形化GUI庫Tkinter分別編寫了基本蟻群算法和最大最小蟻群算法,程序界面如圖1所示。
圖 中 每 個 站 點 上 方 的 五 元 組( β k,1, β k,2 ,β k,3 ,β k,4 ,β k,5 )表示當前醫療箱 k 中5件藥品的偏差值,其中黑色填充的結點代表貨車的起始結點。以使用基本蟻群算法,設置螞蟻種群數q=50,貨車最大負載量 Maxload =800,信息啟發因子 α =1.0,期望啟發因子 β =1.0,信息素強度 Q =100為例,得到的最優調度總距離為4501,調度路徑如圖2所示。
為了比較基本蟻群算法(AS)和最大最小蟻群算法(MMAS)在該問題上的效果,本文分別就不同的貨車最大負載量 Maxload ,分別使用兩種算法進行了檢驗,尋找到的最優路徑長度如表2所示。
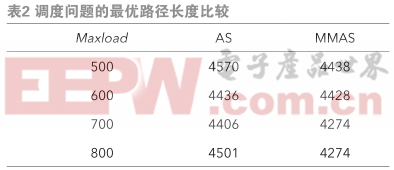
可見,最大最小蟻群算法(MMAS)往往能夠得到比基本蟻群算法(AS)更優的解;此外,貨車最大負載量Maxload 也會在一定程度上影響到最優調度路徑。
4 結論
本文針對一種新型物聯網醫療箱系統,提出了一套使用機器學習和蟻群算法的藥物調度方法,使用嶺回歸、隨機森林回歸和神經網絡的混合算法建立了藥品需求量的預測模型,并使用基本蟻群算法和最大最小蟻群算法對藥品的調度問題進行了求解。該方法為物聯網醫療箱系統提供了一種有效的解決方案,簡化了日常運營維護的過程。此外,在其他的調度問題中,該方法也提供了一種可參考的解決思路。
致謝
最后感謝上海大學機電工程與自動化學院“挑戰杯”大學生課外學術科技作品競賽項目對本文的研究所提供的支持。以及上海大學“羅姆杯”大學生機電工程創新設計大賽對本文研究的支持。
參考文獻:
[1] 趙安琪.自動售藥機破冰之路[J].中國藥店,2010(10):32-32.
[2] 陳雷毅,潘榮,許強,等.高校校園自動售藥機的再設計[J].大眾文藝,2016(11).
[3] Zhao G, Luo W, Sun R, et al. A Modified Max-Min Ant System for Vehicle RoutingProblems[C]// International Conference on Wireless Communications. IEEE, 2008.
[4]段海濱.蟻群算法原理及其應用[M]. 北京 科學出版社,2005.
[5] Stützle T,Hoos H H.MAX–MIN ant system[J]. Future generation computer systems, 2000,16(8): 889-914.
[6] 陳昌敏,謝維成,范頌頌.自適應和最大最小蟻群算法的物流車輛路徑優化比較[J].西華大學學報(自然科學版),2011,30(3).
[7] 李勇,段正澄.動態蟻群算法求解TSP問題[J].計算機工程與應用,2003,39(17):103-106.
[8] 柴寶杰,劉大為.基于粒子群優化的蟻群算法在TSP中的應用[J].計算機仿真,2009,26(8):89-91.
[9] Peter Harrington. Machine learning in action [M].2013.
[10] Liaw A, Wiener M. Classification and regression by randomForest[J].R news,2002,2(3):18-22.
[11] Bose N K, Liang P.Neural Network Fundamentals with Graphs,Algorithms,and Applications(McGraw-Hill Series in Electrical Computer Engineering)[J].1996.
[12] Balki? Z, ?o?tari? D, Horvat G. GeoHash and UUID identifier for multi-agent systems[C]//KES International Symposium on Agent and Multi-Agent Systems: Technologies andApplications. Springer, Berlin, Heidelberg, 2012: 290-298.
[13] Cassel M, Lima F.Evaluating one-hot encoding finite state machines for SEU reliabilityin SRAM-based FPGAs[C]//On-Line Testing Symposium, 2006. IOLTS 2006. 12th IEEEInternational. IEEE, 2006: 6 pp.
作者簡介:
通信作者:李晉,男,上海大學機電工程學院實驗師,碩士,主要從事微控制器技術,人工智能算法應用優化。
第一作者:盧嘉軒,男,上海大學計算機學院本科生,主要從事人工智能算法研究。
第三作者:周延,男,上海大學計算機學院本科生,主要從事人工智能算法研究。
本文來源于科技期刊《電子產品世界》2019年第7期第80頁,歡迎您寫論文時引用,并注明出處






評論