基于主動控制的自適應同步策略在混沌信號解調中的應用

摘要：在保密通信領域，對隱藏在混沌信號中的信息解調是一個重要課題。為了有效地解調信息，提出一種基于主動控制的自適應同步策略。利用Lyapunov穩定性理論和Chua電路模型的數值仿真證實了該策略的可行性。仿真結果表朗在接收器上利用這種策略所設計的主動控制器和自適應解調器能夠提取隱藏于混沌信號中的傳輸信息，并且通過提高主動控制器的增益，可以減少由于外部噪聲和信息的不連續性造成的誤差。
關鍵詞：保密通信；信息解調；主動控制；自適應同步策略；數值仿真

混沌信號以其所固有的難以預測性和對初始值的極端敏感性為混沌在保密通信中的應用提供了前提。美國海軍實驗室研究人員Pecora和Carroll于1990年首次提出了驅動一響應混沌同步方法以及混沌同步控制理論，這為混沌應用于保密通信提供了理論基礎。近十多年來，利用混沌進行保密通信的研究已成為混沌應用研究的一個重要領域。目前已經提出了多種混沌保密通信方案，例如，混沌遮掩法：以混沌信號作為載體來隱藏或遮掩待傳送的信息信號；混沌參數調制方法：用信息信號調制混沌系統的參數來實現調制目標；混沌開關鍵控方法：根據混沌系統在不同參數下具有不同吸引子的特征，把二元信息分別映射到不同的混沌吸引子上以實現保密通信等。

1 保密通信系統
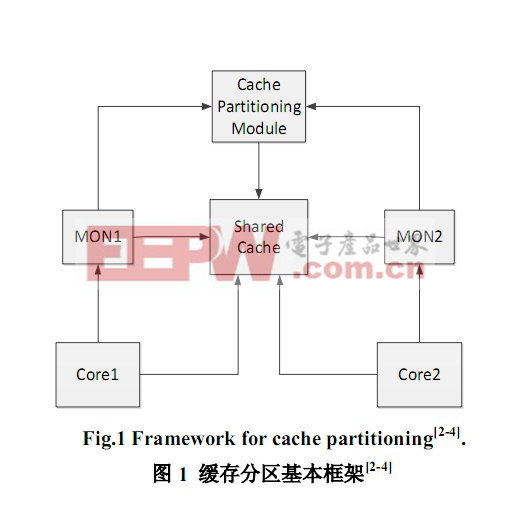
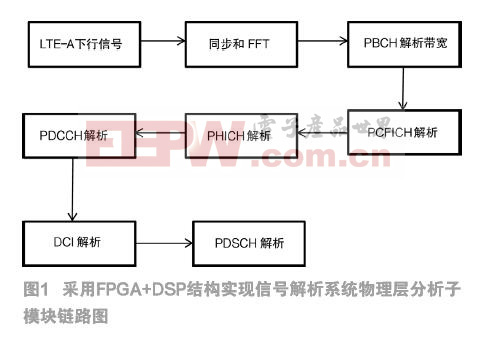
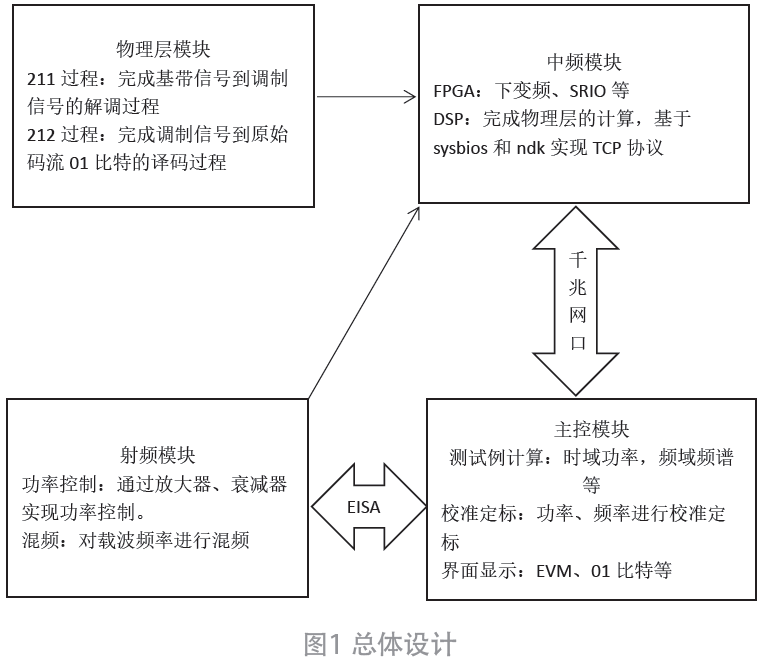
保密通信系統的結構框圖如圖1所示，其中發射機的驅動系統是一個混沌系統，可以描述為：

式中，狀態向量X∈Rn表示傳輸的信號，μ∈Rm為參數向量，F為一個非線性向量函數，s表示要通過混沌系統加密傳輸的有用信息。

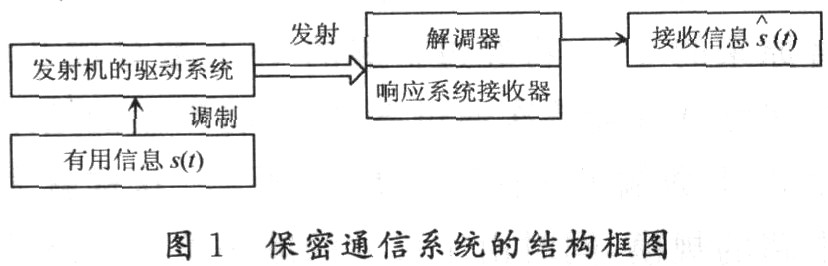
為了能讓該信息安全地到達指定的接收器，必須把它經過混沌驅動系統加密。同時，接收器需要一個專門能檢測出混沌信號的響應系統和一個能解密有用信息的解調器。
驅動系統的狀態向量可表示為：

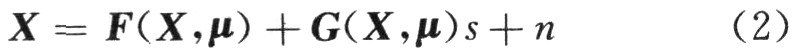
式中，G是一個已知的非線性向量函數，n是外部噪聲。
接收器響應系統的狀態向量與式(2)相同，對于接收器來說，隱藏于混沌信號中的有用信息是不可知的，所以需要一種專門的解調器去解密。

2 解調信息的自適應同步策略
為了從混沌信號中提取有用信息，需要設計一個控制器u和一套實時更新的規則，來使響應系統和驅動系統中的混沌信號保持同步。控制器響應系統的狀態向量可表示為：

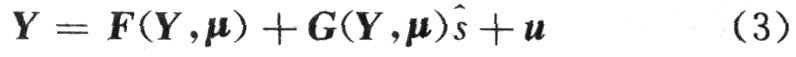
式中，Y是響應系統的輸出信號，s是從混沌信號中經過解密得到的有用信息。
式(3)和式(2)之差是響應系統和驅動系統之間的誤差，它們之間的關系可表示為：

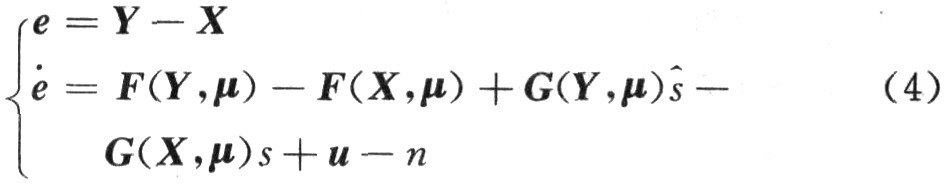
根據以上分析，提出一種基于主動控制的自適應同步策略，據此來設計控制器和解調器。
控制器的設計如下：

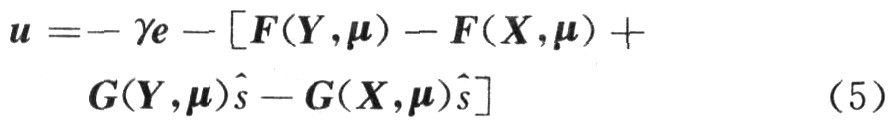
式中，主動控制器的增益γ為正實數。
解調器的設計如下：

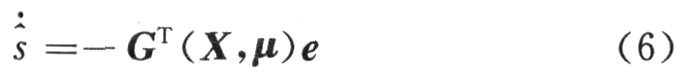
接下來根據Lyapunov穩定性理論來研究系統的穩定性。選擇如下的Lyapunov函數來分析系統的誤差：

顯然，這里的V(e，s)是一個非負函數。根據上述設計的控制器和解調器，可以得出關于V(e，s)的一個推論：

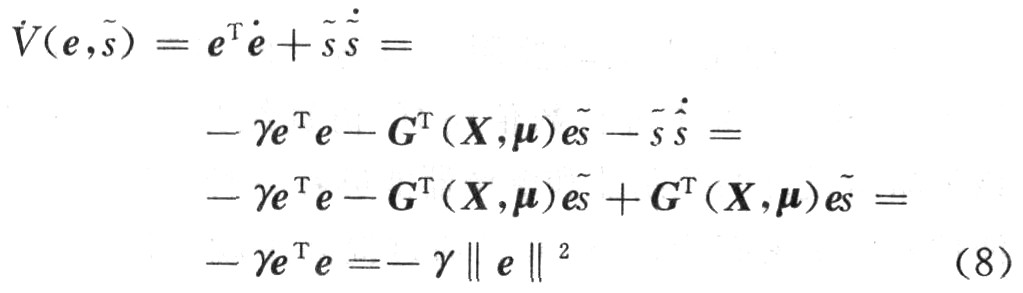
由式(8)可得，當且僅當||e||2=O時，V(e，s)=O，否則會出現V(e，s)0的情況。由此可以推出：當t→∞時，s(t)→s(t)或e→O。這說明解密得到的信息與原始信息非常接近，而且隨著時間的推移，系統的誤差接近于零，即該誤差是大范圍漸進穩定的。因此，從理論上講接收器采用這種設計的控制器和解調器能夠從混沌信號中解密有用信息。

3 接收系統的建模與數值仿真
3．1 接收系統的建模
根據Chua電路的傳輸模型：

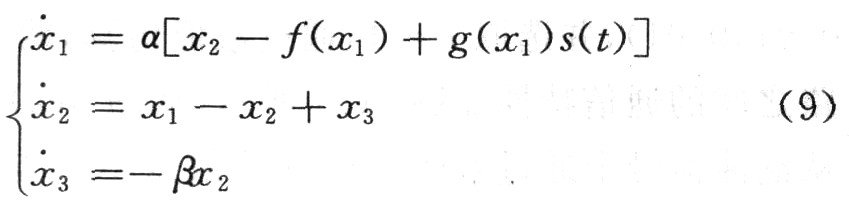
式中，f(x1)=2／7xl一3／14(|x1+1|―|x1―1|)是一個分段線性函數，g(x1)=|x1+1|―|x1一1|。
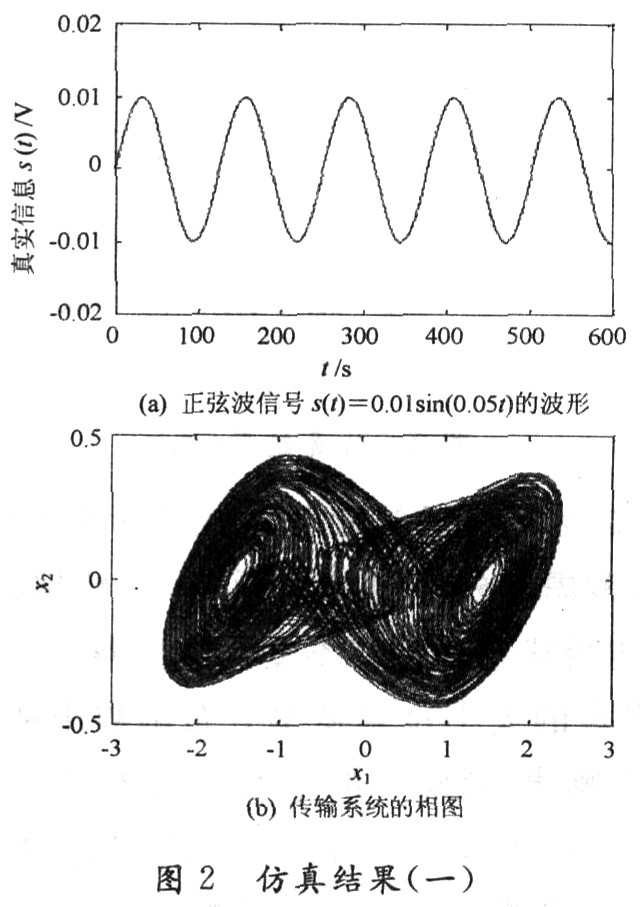
當α=9．0，β=14．286時，上述模型呈現出一種雙螺旋特征。令信息為正弦波信號s(t)=O．01sin(Q，05t)，如圖2(a)所示。假設Chua電路傳輸模型的初始條件為(x1(O)，x2(O)，x3(O))=(1，0．01，0．01)。傳輸系統的相圖(x2比x1)如圖2(b)所示。由圖2(b)可以看出該傳輸系統是混沌系統。因此，包含信息s(t)的混沌信號和不包含信息s(t)的混沌信號是很難進行區分的。

根據上述的主動控制自適應同步策略，接收器模型建立如下：

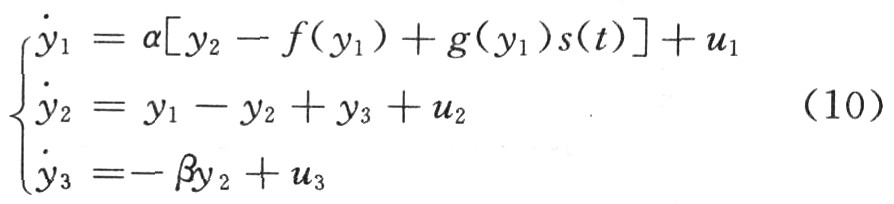
根據式(5)，控制器的參數模型向量u=[u1，u2，u3]T的設計如下：

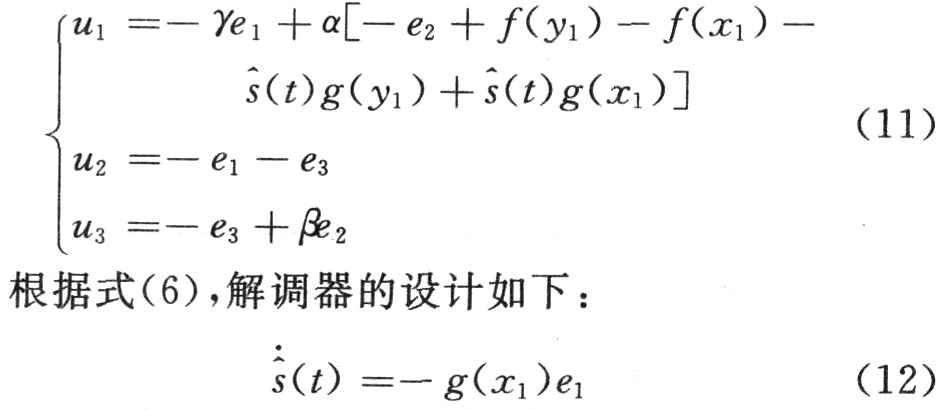
3．2 無噪聲混沌系統的連續信號數值仿真與結果分析
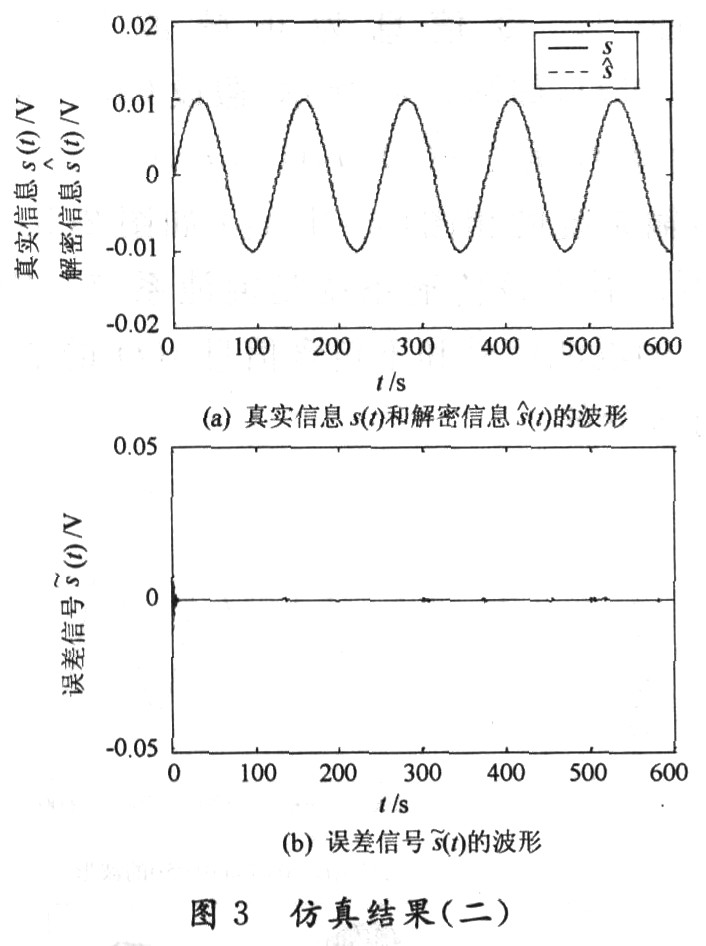
首先，假設在沒有噪聲的情況下，傳輸的信息為圖2(a)所示的正弦波信號s(t)=0．01sin(O．05t)，響應系統的初始狀態為(y1(O)，y2(O)，y3(0))=(一1，0．01，O．01)，并選取γ=1，通過數值仿真，兩個Chua電路之間的通信特性如圖3(a)所示。從圖3(a)可以看到從混沌信號中通過解密所得到的信息s(t)與真實信息s(t)幾乎是完全重合的。從圖3(b)可以看到隨著時間的推移，誤差信號s(t)=s(t)一s(t)迅速降低到幾乎接近于零的值。

3．3 帶噪混沌系統的連續信號數值仿真與結果分析
其次，考慮在外部噪聲的影響下，傳輸的信息和響應系統的初始狀態均保持不變。．假定噪聲n(t)=ρ?σ，其中ρ為噪聲的大小，σ是概率分布函數服從N(0，1)分布的高斯白噪聲，該噪聲的平均值為零，標準方差為1。取ρ=0．02 V，當γ=1和γ=5時，通過數值仿真，這時兩個Chua電路之間的通信特性與圖3(a)基本相同，其誤差信號s(t)的波形如圖4所示。

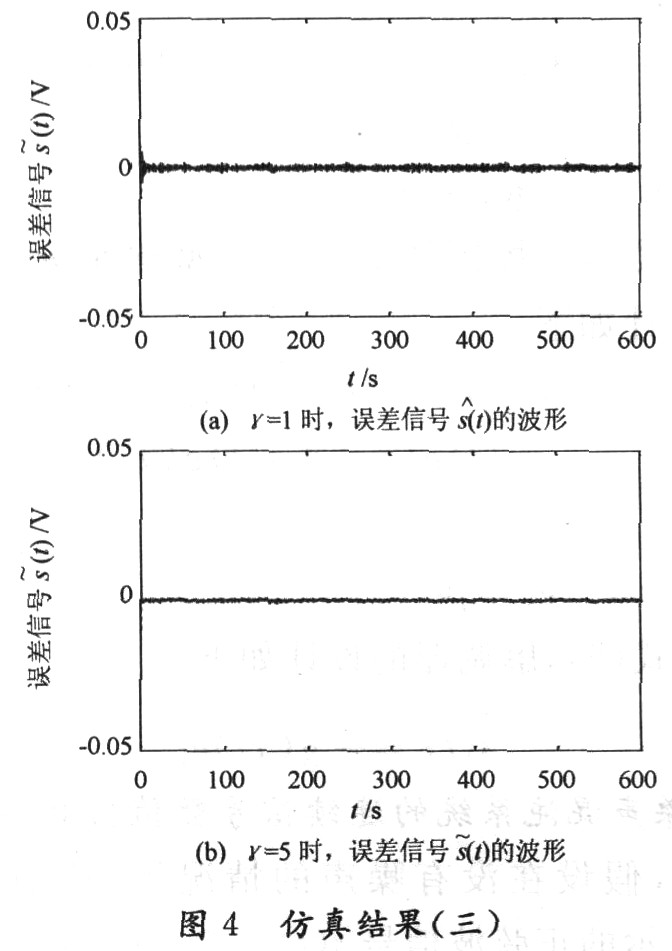
從圖4可以看出即使在外部噪聲的影響下，產生的誤差依然很小。從混沌信號中通過解密所得到的信息s(t)與真實信息s(t)保持較高的一致性。此外，通過圖4(a)和圖4(b)的對比可以看出，提高γ的值還可以進一步地減小由于噪聲所帶來的誤差。
3．4 不連續信號在混沌系統中的數值仿真與結果分析
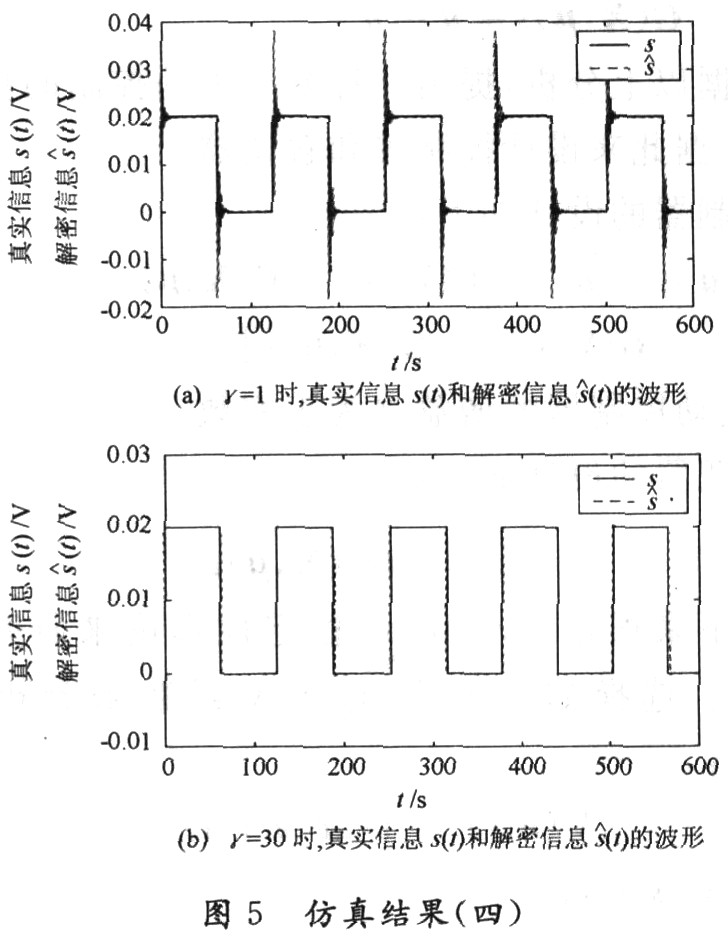
最后，考慮不連續信號的情況。令信息為不連續的方波信號s(t)=0．01[1+sign(sin(O．05t))]，響應系統的初始狀態為(y1(0)，y2(0)，y3(O))=(一1，O．01，0．01)，并選取γ=1，通過數值仿真，這時兩個Chua電路之間的通信特性如圖5(a)所示。從圖5(a)中可以看出解密所得到的信息s(t)與真實信息s(t)相比，由于信息的不連續性，誤差非常明顯。同樣可以通過提高γ的值來減小誤差，其仿真結果如圖5(b)所示。

4 結 語
提出一種基于主動控制的自適應同步策略，并在Matlab／Simulink中進行數值仿真，仿真結果表明，根據該策略所設計的控制器和解調器能夠在各種情況下從混沌信號中解密有用信息，并且通過提高主動控制器的增益可以很容易地減少由于外部噪聲和信息的不連續性引起的誤差。可以預計，隨著混沌理論的不斷完善和發展，混沌理論必將在混沌通信領域發揮更大的作用。