基于改進的神經網絡油田配電網諧波預測研究

傳統BP網絡收斂速度慢,很難實現大量樣本數據的處理及應用與進行實時預報。因而,與以往常規的梯度下降法不同,本文修正BP網絡的閾值和連接權值采用Levenberg-Marquardt算法(簡稱L-M算法)。L-M算法的基本原理如下:

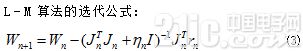
式中:I為單位陣;為一個非負值。依賴于的幅值,該方法光滑地在兩種極端情況之間變法:即Guass-Newton法(當0)和標準梯度法(當)。該式即可作為BP神經網絡的學習訓練方法。

網絡權值和偏差的變化量:

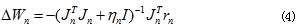
并以此不斷來對網絡進行調整訓練,直至達到目標要求。由式(3)可知,L-M法實際上綜合了Newton法和標準梯度下降法二者的優點,是Newton法和標準梯度下降法的結合。因而,以L-M算法設計的BP網絡在精度及收斂速度方面都有很明顯的優勢。

根據公式(2)模型中的假設,訓練過程中,輸入為總的電流值和基波電流值,根據采樣時間的不同每個周期選擇8對樣本,基波的幅值上限定位1.0,模型的輸出為0.02、0.05和0.5幅值的5次諧波,這樣輸入共24對采樣樣本。

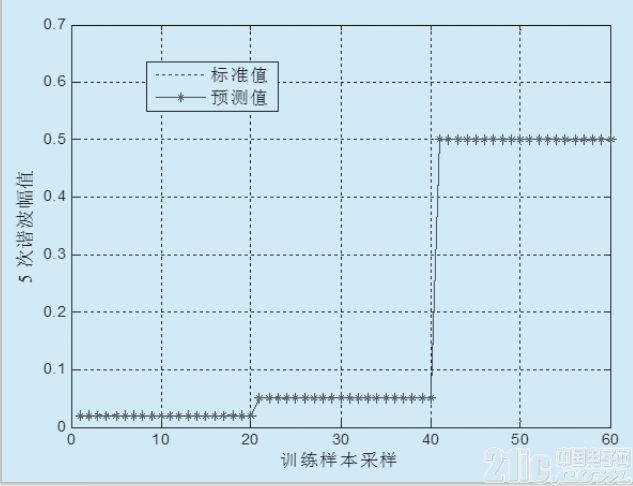
圖2 基于L-M算法的BP神經網絡

諧波預測模型建立

基于L-M算法的網絡模型訓練過程如圖2所示,基于24對訓練樣本的的模型平均誤差為0.0085,達到了一定的精度。為驗證網絡的泛化能力,重新生成40對樣本,輸出諧波幅值分別是0.4和0.08,仿真結果如圖3所示。文中仿真數據采用階躍跟蹤信號,神經網絡模型的仿真結果驗證了L-M算法具有梯度法的全局特性,提供了牛頓法的速度和保證收斂的梯度下降法之間的折衷,收斂的迭代次數少,能快速完成網絡訓練。

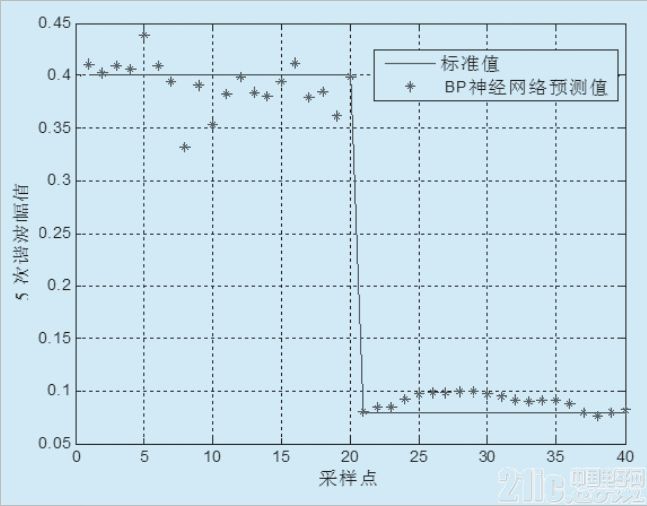
圖3 基于L-M算法的BP神經網絡

諧波預測誤差

5 結束語

本文結合油田的實際需求,建立了油田配電網簡化的數學模型,以五次諧波為研究對象,設為神經網絡的輸出進行仿真研究,采用改進的BP神經網絡方法對油田配電網諧波進行預測預報,并進行了測試樣本驗證。仿真結果驗證了L-M算法的優越性,本文提出的神經網絡預測油田配電網諧波能減少諧波污染,非常具有實用價值。因此,本課題的研究將對于我國在油田節能供電方面技術的提升、供電質量的提高以及高性能供電技術的發展都具有很大的意義,為使電能能夠在油田中得到高效、低污染的應用開辟重要途徑。