基于貝葉斯博弈的無人機通信延時研究

摘要：在無人機通信網絡中，無人機之間協同通信已經成為重要的研究方向。本文針對無人機類型的不確定性，基于動態貝葉斯聯盟博弈，通過計算無人機在最小通信延遲下的收益，利用貝葉斯聯盟博弈來分析無人機的策略選擇。此外，利用信念更新機制來發現系統中潛在的聯盟成員。仿真表明，獲得的聯盟結構是納什穩定的。

引言

　　多無人機(unmanned aerial vehicle，UAV)協同搜索是多無人機協同的一個重要研究方向。多架UAV同時對一個未知區域進行搜索，目的就是大量獲取搜索區域的信息，確定目標存在的具體位置。文獻[1]提出了一種基于貝葉斯理論的多UAV魯棒協同搜索方法，首先建立搜索環境的數學模型，然后考慮到UAV傳感器測量的不確定性以及環境自身的不確定性，引入魯棒性能參數以提高系統的抗干擾性以及穩定性，最后對目標函數進行優化求解，從而引導UAV在區域中進行搜索。任務集結是協同作戰的首要行動和自組織協同控制的重要內容，文獻[2]為優化集結行動中系統任務狀態協調過程能量最優性、協同控制動態響應性和集結行動時效性3個性能指標，采用基于快速一致性控制算法的協同控制結構，在合作博弈框架下給出多無人機系統自組織協同與優化控制問題描述，建立了優化控制輸入的Pareto解集，采用Nash討價還價方法給出基本合作博弈優化一致性控制算法。在基本算法中引入過去狀態差值，并以優化目標構建適應度函數，采用遺傳算法優化代價函數的加權矩陣，得到改進合作博弈優化一致性控制算法。文獻[3]通過考慮合作聯盟的目標價值收益指標函數、損傷代價指標函數及航程代價指標函數，建立多無人機聯盟合作博弈模型，構建出其博弈矩陣，給出合作聯盟特征函數與混合策略納什均衡的定義，采用粒子群算法(particle swarm algorithm，PSO)求解出混合策略的納什均衡，并利用Shapley 值方法，給出一種合作博弈的求解方法，最終得到多無人機對地攻防最優對抗策略。文獻[4]對目標運動行為的綜合利用，以敵我雙方為局中人，把敵我雙方可能的行為作為策略集，建立博弈論模型，通過求解Nash均衡改進掃描式搜索路徑規劃算法。文獻[5]通過分析實際戰場中目標價值和毀傷概率信息的不確定性，提出了不確定信息條件下需要解決的無人機(UAV)攻防博弈問題。以敵我雙方發射導彈的價值信息為依據，建立基于不確定信息的多UAV攻防對抗的支付函數，構建攻防雙方博弈支付矩陣。將粒子群算法和區間數多屬性方案排序方法相結合，給出基于不確定信息下博弈納什均衡求解方法，為不確定環境下UAV攻防博弈實現最優策略提供了新方法。

　　現在我們考慮一些無人機為降低傳輸成本，提高自身的利益，會出現不良行為的無人機。無人機的行為有兩種類型：協作的無人機總是會協助聯盟內其他無人機進行信息傳輸;不良行為的無人機則表現為在聯盟內有時會不參與其他無人機的協作信息傳輸。為了模擬存在協作無人機和不良行為無人機間的聯盟形成過程，建立了基于貝葉斯聯盟博弈^[6]模擬無人機間協作傳輸信息的過程。

1 系統模型

　　如圖1所示為無人機目標系統，各個無人機之間能夠形成聯盟并在彼此間共享目標信息。假設各個無人機位于不同的高度，避免了他們彼此間的碰撞^[7]。

　　無人機的運動模型：

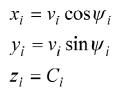(1)

　　其中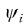，是角度，v_i是對地速度，c_i是常數對應每個無人機的高度，考慮兩種類型的無人機成員：協作的無人機和不良行為的無人機。

2 貝葉斯聯盟博弈建立

　　我們利用貝葉斯聯盟博弈形成處理無人機類型的不確定算法^[8]。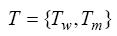表示無人機可能的類型集合，T_w代表協作的無人機，T_m代表不良行為的無人機。

　　無人機i的預期收益：

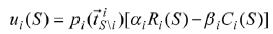(2)

　　其中a_i表示平均效用的權重系數，β_i表示平均成本的權重系數。對于無人機i來說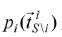，是其對同聯盟S內其他無人機的聯合信念概率，其計算如下：

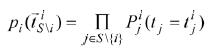(3)

　　無人機i的效用表示為R_i(S)：

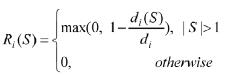(4)

　　其中，d_i(S)表示無人機i加入聯盟S后信息傳輸延時，d_i=d({i})表示無人機i不加入任何聯盟的信息傳輸延時。

　　無人機i傳輸目標信息到同聯盟任何無人機j引起的平均成本為：

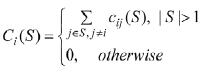(5)

　　其中，c_ij(S)表示無人機i傳送目標信息到聯盟S內無人機j的平均成本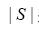，表示聯盟S中無人機的數量。

　　為了更多獲知不完全信息下無人機的類型，根據當前時隙和歷史信念[8]的結果，通過貝葉斯定理^[9]，每個無人機更新關于其他無人機類型的信念概率。θ=0代表不合作，θ=1代表合作。

　　其中，率。

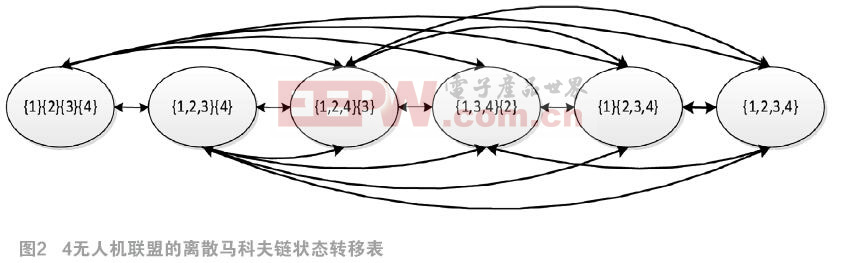
3 基于離散馬爾科夫鏈的聯盟形成穩定性分析

　　當每個無人機從自身的效益值角度進行聯盟組合的調整時，那么狀態(聯盟結構)之間的變化可以運用馬爾科夫鏈[^10]的方法進行分析，以驗證貝葉斯聯盟形成算法的穩定性。

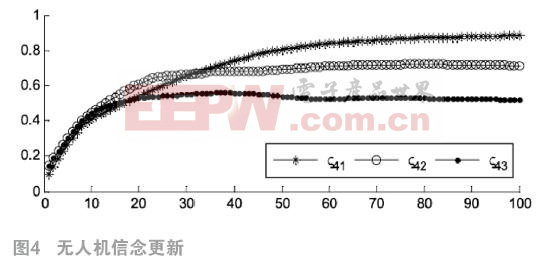
本文來源于中國科技期刊《電子產品世界》2016年第9期第52頁，歡迎您寫論文時引用，并注明出處。