技術分析：時鐘寬帶GSPS JESD204B ADC

　　隨著使用多模數轉換器(ADC)的高速信號采集應用的復雜性提高，每個轉換器互補時鐘解決方案將決定動態范圍和系統的潛在能力。 隨著新興每秒一千兆樣本(GSPS) ADC的采樣速率和輸入帶寬提高，系統的分布式采樣時鐘的能力和性能變得至關重要。 以高頻測量為目標的系統解決方案，例如電氣測量儀器儀表和多轉換器陣列應用，將需要尖端的時鐘解決方案。

　　選擇專門的輔助時鐘解決方案對防止ADC動態范圍受限非常重要。 根據目標輸入帶寬和頻率，時鐘抖動可能會反過來限制ADC的性能。 轉換器的高速JESD204B串行接口的低抖動和相位噪聲、分配鏈路和對齊能力都是對優化系統性能極其重要的時鐘屬性。

　　支持帶JESD204B輸出ADC的多通道低抖動GHz時鐘解決方案繼續在業內激增。 設計工程師問我們該如何為其GSPS ADC選擇合適的時鐘解決方案。 下面就是答案和對與將時鐘解決方案與特殊ADC配對產生的技術影響相關的部分常見討論的分析。

　　第2或第3奈奎斯特頻率區域對寬帶GSPS ADC使用高輸入頻率需要較低的抖動和高速時鐘。 時鐘抖動對ADC性能有什么影響?

　　由于采用GSPS ADC和直接RF采樣的系統中使用高頻率輸入信號，因此時鐘抖動對系統性能的影響越來越大。 固定量的時鐘抖動可能不會對具有低頻輸入的系統性能產生限制。 隨著ADC輸入頻率提高，相同固定量的時鐘抖動會對系統的信噪比(SNR)產生影響。 ADC的SNR定義為信號功率或噪聲與輸入ADC的總非信號功率的對數比。

　　在較高頻率下對快速上升時間信號進行采樣時，具有已知量時鐘抖動的ADC采樣時刻將產生更大或更模糊的采樣電壓增量(dV)。 這是因為，高頻信號的壓擺率比低頻信號大。 圖1所示為這種關系的一個示例：

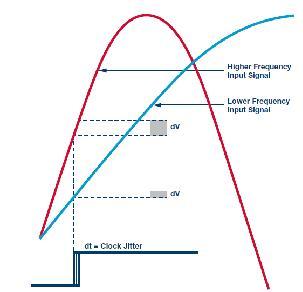
　　圖1

　　ADC時鐘出現固定量的時鐘抖動(dt)后，更高頻率的輸入信號將具有一個更大的采樣電壓誤差dV，此誤差與更低頻率的輸入信號相關聯。 這會對ADC的動態范圍能力產生直接影響。

　　峰峰值和rms(均方根即平方)抖動之間的區別是什么?

　　時鐘信號有兩類抖動會直接影響ADC的性能： 隨機抖動(RJ)和確定性抖動(DJ)。 確定性抖動源自一個可識別的干擾信號，其幅度大小是有界的。 它由所有其他無用信號特性產生，這些特性包括串擾、電磁干擾(EMI)輻射、電源噪聲以及同步開關等周期性調制。 確定性抖動在時鐘信號上將表現為雜散信號。 這些無用信號還會在ADC產生的數字頻譜上表現為雜散信號。

　　隨機抖動的大小沒有界，而且是高斯抖動。 它可由較不可預測的影響產生，例如溫度和小型半導體工藝變化。 如果ADC采樣時鐘上存在足夠的隨機抖動，則可能提高數據轉換器上的噪聲頻譜密度(NSD)。 將每個RJ和DJ均方根的大小(RSS)相加便可以確定全部抖動對ADC采樣時鐘的影響。

　　典型時鐘信號上的隨機抖動大小直方圖應為完全正常的高斯分布。 抖動的任何附加確定性分量都將產生雙峰分布。 通過進行大量時序測量并確定最小和最大的抖動偏差，可測量峰峰值抖動。 隨著更多測量的進行，最小和最大抖動將最終繼續擴大絕對峰峰值。 有效的測量必須是固定的時間和測量樣本數量。 因此，絕對峰峰抖動值并不是特別有用，除非是基于標準偏差已知的高斯分布。

　　均方根抖動是高斯曲線內一個標準偏差的值。 即使被測樣本大小增加，該值也幾乎不會變化。 這也意味著，均方根抖動值比峰峰抖動值更有意義，并且更易測量。 要使均方根抖動的大小有意義，總抖動必須是高斯分布。 變形的高斯分布圖表示存在確定性抖動分量。 如果可能，應識別出確定性抖動分量的根本原因并將其緩和或消除。

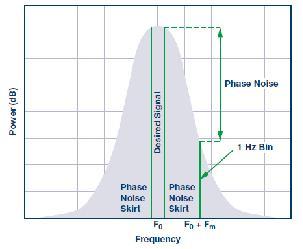
　　圖2

　　盡管一個理想時鐘信號的所有功率均應在單個頻點內，但實際的時鐘解決方案會有一些“相位噪聲波裙”大小。 只有隨機抖動的時鐘信號將形成高斯分布。 任何確定性抖動都將使理想的高斯分布圖變形。 曲線上任意點的相位噪聲功率可從F0處的峰值到F0 + Fm處的目標頻點測得。

　　ADC的輸入時鐘抖動將如何降低SNR和NSD的性能?

　　ADC的NSD是轉換器的主要性能指標之一。 NSD定義單位帶寬條件下的整個噪聲功率(在相應ADC采樣頻率(fS)采樣)。 NSD是ADC的滿量程信噪比(SNRFS)與任意時鐘抖動下降和噪聲分布于頻譜的奈奎斯特帶寬(fS/2)的函數。 任意采樣時間誤差都將導致噪聲信號功率的某些部分下降。

　　隨著時鐘抖動增加，目標采樣信號功率的某些部分將以快速傅里葉變換(FFT)散布到其分立頻點外，隨后將變為噪聲功率的一部分。 這是因為時鐘信號相位噪聲附近的信號的采樣時間不理想。 圖2顯示了相位噪聲“波裙”如何從頻域中的理想目標信號泄放功率的直觀示例。

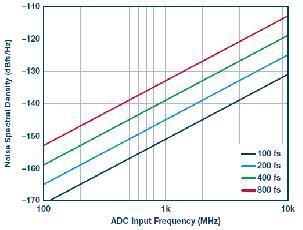
　　圖3

　　以1 GSPS工作的ADC的理想NSD性能受rms編碼時鐘抖動限制。 時鐘的均方根抖動可能會限制ADC在更高輸入頻率下的動態范圍。

　　要得到ADC的總SNR下降值，應計算抖動噪聲功率和ADC在目標信號頻率下的標準SNR的和的平方根。 當ADC采樣時鐘抖動足夠低時，SNRadc = SNR下降，因為轉換器的內部孔徑抖動和非線性將限制其SNR。 相反地，抖動逐漸增大的采樣時鐘將最終變成ADC SNR性能的限制因素。 這會越來越明顯，因為目標信號的頻率更高。 所有可實現ADC的輸出噪聲受SNR性能限制。 隨著輸入電平增大或減小，抖動噪聲分量將相應地變化。

　　ADC的NSD可通過將ADC的滿量程輸入功率減去噪聲功率的SNR下降值計算出，SNR下降值是奈奎斯特頻率的函數。 通過下式可得出此值。

　　NSDADC = PowerADC_FS– SNR下降(dBFS) – 10log(fS/2)

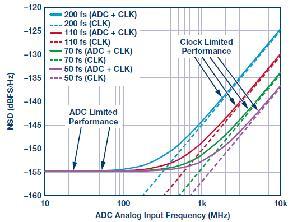
　　圖4

　　此圖顯示了一個14位寬帶轉換器，該轉換器在低模擬輸入頻率(<100 MHz)下被內部ADC量化和線性限制為–155 dBFS/Hz NSD，無論外部均方根時鐘抖動是否達到200 fs。 這種情況下，系統時鐘抖動將根據其均方根幅度確定高模擬輸入頻率(>100 MHz)下的NSD性能。