加快誤碼率測試的置信度和精度估算方法
FB100A (除數據和時鐘端口及其補碼外)還有兩個端口或通道。這些額外的端口可用作一個或兩個附加控制線,即幀結構同步通道及其補碼;或單端幀結構同步信道及附加單端幀結構數據有效指標同步控制線。這些附加的端口可用于測試在設計中包含這些控制線的簡單數據接收機,避免增加前期的硬件投入。
FB100A 的另一項重要性能是儀表的內部數據發生器和數據分析儀可以用作單獨的儀表。發生器產生的數據可以不同于分析儀分析的數據。當需要分析從被測設備(而不是 FB100A)發出的信號時,這是一個重要的工具。這一性能是因為FB100A中發生器和分析儀分別使用了單獨的4M字節內存。對于多功能的控制線功能, FB100A數據發生器擁有附加的4M字節可編程內存,用于獨有的幀結構同步序列。
最后,FB100A在物理層方面的多功能性為用戶提供了邏輯接口界面的多種不同選擇。串行通訊方式中,標準輸出提供TTL和ECL,或TTL和PECL邏輯電平。并行通訊方式,用戶可購買各種 POD選件,包括了字節寬度的數據和控制線。這些并行POD通過FB100A標準物理邏輯接口提供用戶設備的連接。接口包括:使用SPI(同頻串行接口) 的MPEG,ASI(異步串行接口),或RS422,還有更為通用的串行數據傳輸,如RS232、RS449和HSSI,包含如TTL和LVDS邏輯電平。
當加入開始提到的通用數據發生器和協議分析儀等設備的功能,FB100A的上述性能使得簡單的誤碼率測試設備可以成為功能強大的通訊分析工具。
AWGN和高斯概率分析
理論上,你可以測量無限長時間得到精確的誤碼率測試結果。然而,實際上你需要相對短的時間進行測試。因此,真實的BER統計可能明顯高于或低于你的測試結果。
通過加入已知統計概率的權重到系統中,你可以通過已知的概率分布描述誤碼的發生。使用概率分布,你可以簡單地用可信度水平和實際精度估算描述單個測試。這種方法可以在可接受的不確定度下,在短時間內得到可重復的測試結果。
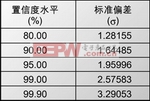
在給出公式之前,回顧一下置信度水平和精度估算會很有幫助。置信度水平定義了實際誤碼率包含在你測試的精度范圍內的概率。精度與測試誤碼率和真實誤碼率的差有關。你通常用百分數來表示它。
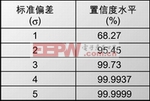
作為一個樣例,假設你作一個測試,記錄了100位誤碼。如果設定置信度水平是一個標準偏差(或68.27%),測試精度是10%。也就是說,真正的誤碼率落在誤碼率測試結果10%范圍內的可能性有68.27%。如果你測試了10,000次,有6,827次在測試結果誤差10%范圍內,其余3,172次超出測試結果10%的范圍。
使用高斯概率分布計算誤碼率測試參數
高斯概率分布提供了一個包含置信度水平和精度估算的公式,可用于誤碼率測量。基本公式把置信度水平和精度估算與實際測得的誤碼數關聯起來。你可以使用其中兩個參數,使用這個公式解決任何包含三個參數的問題。更多的,你用它解決精度估算,但它也可解決給定精度和置信度水度時需要測得多少誤碼的問題。本文介紹的第二個公式描述了最少的無誤碼測試時間與可信的理想誤碼上限的關系。
第一個公式在假定誤碼不為零的情況下,為期望的精度估算提供一個計算方法。執行這個計算時,你還必須設定置信度水平。這個等式解決了測量精度問題,可以表示為 ± 誤差,用于誤碼率測試。這個誤差因素與測試時間和誤碼率無關,它只取決于測試的誤碼位數。
精度 =s/vn
s:標準偏有效期 n:誤碼位數
標準偏差直接與置信度有關。表1和表2給出了置信度水平和標準偏差的關系樣例。上面等式中標準偏差的數值代表了置信度水平;置信度水平代表了真正誤碼率落入你計算的精度范圍內的可能性。
舉個例子,假定一個測試結果有4,331位誤碼位。期望的置信度水平是99.9%,你用3.29053的標準偏差。可以計算出精度大約是5%:
精度=3.29053/v4331
=3.29053/65.8027
=0.050006
你可以用相同的公式確定得到相應精度和置信度所需的誤碼位數。這個等式可以有效地確定何時可以結束測試,當測試的誤碼數量達到這一值時就可以終止測試。解決計算誤碼位數的問題,這個公式可以變為:
誤碼位數=(s/a)/v
s:標準偏差; a:期望的精度
繼續使用前面的樣例,假定目標精度是±5% ,置信度為 99.9%。需要測試的誤碼位數為4,332:
位誤碼率 =(3.29053/0.05 )/v
= 65.81062/v
= 4331.035
注意置信度、精度和誤碼位數在等式中的關系。置信度和精度成反比,而他們兩個同時正比于誤碼位數。基本上,置信度提高,則精度變差或誤碼位數增加。相同的關系適用于精度的增加,置信度下降,或誤碼位數增加。當你在測試前使用公式確定置信度、精度或測試時間,這一概念非常有用。
沒有誤碼時誤碼率參數的計算
前面介紹的公式確定了精度但需要誤碼位數。注意其前提條件是測試時會產生累積的誤碼位數。但是,當測試沒有無誤碼時,會發生什么呢?因為誤碼率是零,設置精度是沒有意義的,因為任何精度乘零結果都是零。你不能假定真實的誤碼率為零,因為你只進行了一個樣本測試。因此你需要找到一條可信的誤碼率上限,用于測量零誤碼的情況。
進行此項測試,你需要考慮另一種不同的概率分布,叫泊松分布。分析泊松分布,你使用一個公式計算一個幾乎不可能再次發生的事件的概率。如果真正的誤碼率是知道的,你可以用公式計算在給定時間內零誤碼的概率:
P(0)=e - rT
R:誤碼位出現的頻率 T:測試時間
這個公式提供了測試零誤碼的概率。這個概率可以轉化置信度。零誤碼概率等于真正的誤碼率等于或高于公式中設定的誤碼率的幾率。因此,如果你變換概率為“1-P(0)”,它變為真實誤碼率等于或低于公式中誤碼率的概率。






評論