基于變結構混沌的偽隨機序列發生器

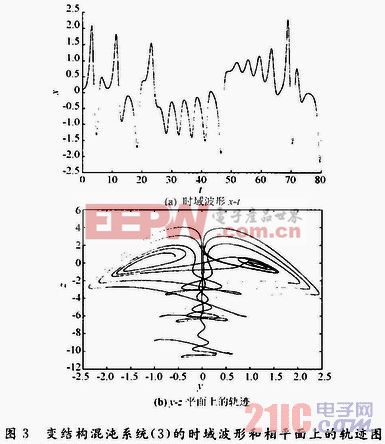
圖3中，實線和虛線分別為為系統(1)和(2)的波形或軌跡。
從圖3看出，該系統的信號波形或解的軌跡由兩個不同的部分構成。當系統的解x≥m=0．2時，u(x-m)=1，混沌系統(3)為混沌系統(2)的結構；當系統的解xm=0．2時，u(x-m)=0，式(3)變為混沌系統(1)的結構，如此往復變化。雖然在這種結構變化中的門限為一確定值，但由于混沌的不可預測性導致何時達到這一門限足無法預知的，即這種結構隨時間而變化的規律是無法預知的，也是隨機的。
這種由兩個不同的混沌信號按時間隨機地混雜在一起而形成的一個完整的混沌信號，比之由單一混沌系統產牛的信號要復雜得多，且門限參數本身又是一種密鑰參數，它擴展了混沌偽隨機序列的密鑰空間，使其提高了安全性。

2 偽隨機序列發生器設計及性能分析
基于上述的變結構混沌系統可設計一種新的偽隨機序列發牛器。主要思路是以變結構混沌系統作為隨機信號源，采用一定的方法對其離散、量化，獲得一系列的偽隨饑序列。
這里研究的變結構混沌系統是一個非線性常微分方程組，在數字系統中對其進行數值解就是一種離散的方法。常微分方程近似求解的數值方法有歐拉算法、改進型的歐拉算法和龍格庫塔法等，這都是將連續系統進行近似離散化的方法。其中，歐拉算法速率最快，本文采用歐拉算法將連續混沌離散化。對于一個連續的混沌系統，有：


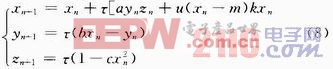
當τ足夠小時，經過歐拉算法離散化后的系統具有與式(3)所示的連續混沌系統相同的動力學特性，此處選擇τ=0．004。
在數字系統中迭代求解式(8)所示的離散化系統，迭代過程中的每一個解變量xn，yn和zn都可以通過二進制數據的方式來表示。以xn為例：

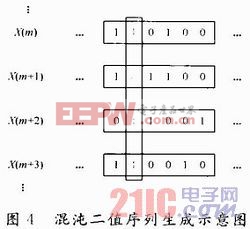
式中：b1n，b2n，…，b(k+1+l)n分別為二進制數的所有位(0或1)，混沌系統的解xn隨時間不斷變化，其二進制表達式中的每一位bm(“0”或“1”)也隨時間小斷變化。如果抽取隨時間變化的一位或多位，可構成一個由“0”或“1”組成的偽隨機序列。為了保證提取的序列具有較好的隨機性，可以嚴格地從小數部分中提取其中一位作為隨機序列，也可以從{b1n，b2n，…，b(k+1+l)n}中選取隨機性能較好的多位作為隨機序列，從而增加隨機序列的提取速度。這種量化方法可用圖4表示。