基于FPGA的高速定點(diǎn)FFT算法的實(shí)現(xiàn)
引 言
快速傅里葉變換(FFT)作為計(jì)算和分析工具,在眾多學(xué)科領(lǐng)域(如信號(hào)處理、圖像處理、生物信息學(xué)、計(jì)算物理、應(yīng)用數(shù)學(xué)等)有著廣泛的應(yīng)用。在高速數(shù)字信號(hào)處理領(lǐng)域,如雷達(dá)信號(hào)處理,FFT的處理速度往往是整個(gè)系統(tǒng)設(shè)計(jì)性能的關(guān)鍵所在。
針對(duì)高速實(shí)時(shí)信號(hào)處理的要求,軟件實(shí)現(xiàn)方法顯然滿足不了其需要。近年來(lái)現(xiàn)場(chǎng)可編程門陣列(FPGA)以其高性能、高靈活性、友好的開發(fā)環(huán)境、在線可編程等特點(diǎn),使得基于FPGA的設(shè)計(jì)可以滿足實(shí)時(shí)數(shù)字信號(hào)處理的要求,在市場(chǎng)競(jìng)爭(zhēng)中具有很大的優(yōu)勢(shì)。
在FFT算法中,數(shù)據(jù)的寬度通常都是固定的寬度。然而,在FFT的運(yùn)算過(guò)程中,特別是乘法運(yùn)算中,運(yùn)算的結(jié)果將不可避免地帶來(lái)誤差。因此,為了保證結(jié)果的準(zhǔn)確性,采用定點(diǎn)分析是非常必要的。
1 FFT算法原理
FFT算法的基本思想就是利用權(quán)函數(shù)的周期性、對(duì)稱性、特殊性及周期N的可互換性,將較長(zhǎng)序列的DFT運(yùn)算逐次分解為較短序列的DFT運(yùn)算。針對(duì)N=2的整數(shù)次冪,F(xiàn)FT算法有基-2算法、基-4算法、實(shí)因子算法和分裂基算法等。這里,從處理速度和占用資源的角度考慮,選用基-4按時(shí)間抽取FFT算法 (DIT)。對(duì)于N=4γ,基-4 DIT具有l(wèi)og4N=γ次迭代運(yùn)算,每次迭代包含N/4個(gè)蝶形單元。蝶形單元的運(yùn)算表達(dá)式為:
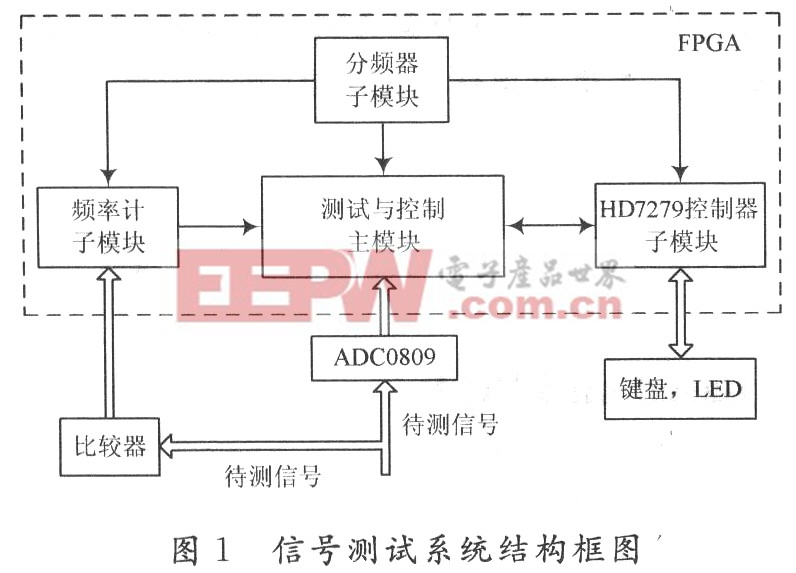
其信號(hào)流如圖1。式中:A,B,C,D和A′,B′,C′,D′均為復(fù)數(shù)據(jù);W=e-j2π/N。進(jìn)行1次蝶形運(yùn)算共需3次復(fù)乘和8次復(fù)加運(yùn)算。N=64 點(diǎn)的基-4DIT信號(hào)流其輸入數(shù)據(jù)序列是按自然順序排列的,輸出結(jié)果需經(jīng)過(guò)整序。64點(diǎn)數(shù)據(jù)只需進(jìn)行3次迭代運(yùn)算,每次迭代運(yùn)算含有N/4=16個(gè)蝶形單元。
2 FFT算法的硬件實(shí)現(xiàn)
2.1 流水線方式FFT算法的實(shí)現(xiàn)
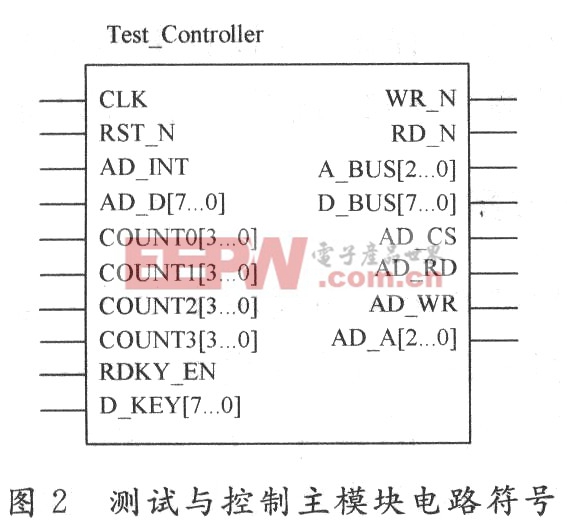
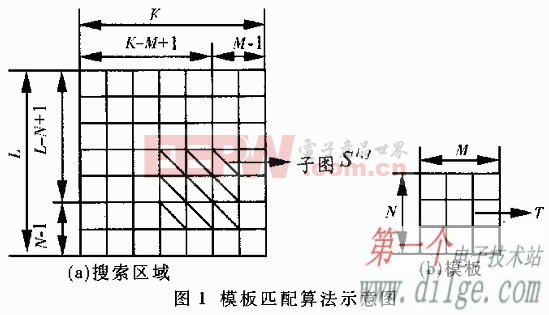
為了提高FFT工作頻率和節(jié)省FPGA資源,采用3級(jí)流水線結(jié)構(gòu)實(shí)現(xiàn)64點(diǎn)的FFT運(yùn)算。流水線處理器的結(jié)構(gòu)如圖2所示。














評(píng)論