基于FPGA的等位移多點采樣硬幣識別研究

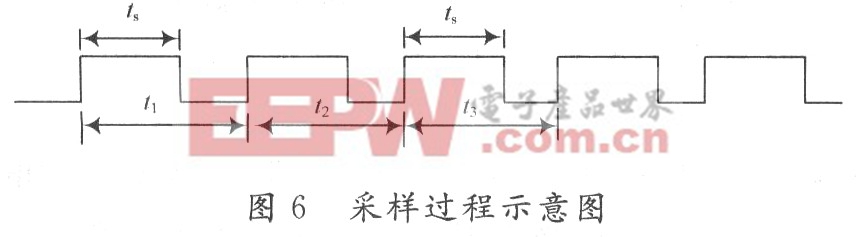
由于硬幣在幣道中做勻加速度直線運動，設硬幣的前沿通過D點時的速度為vD，則有：

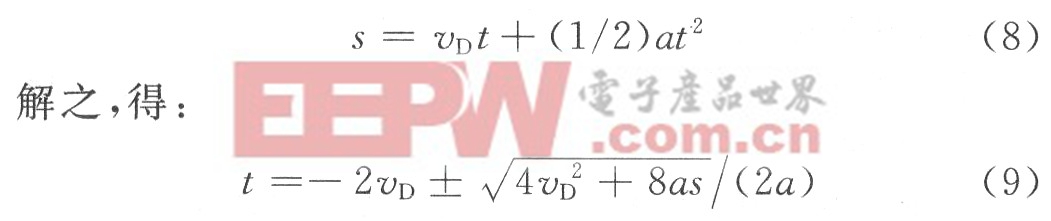
令s為0．1 mm，0．2 mm，0．3 mm，…，設需要的時間分別為t0.1，t0.2，t0.3，…。由2．3所述方法可求得a和vD，則通過求解一元二次方程可得到t0.1，t0.2， t0.3，…，若以硬幣通過D點作為零時間參考點，則在t0.1，t0.2，t0.3，…采樣即可得到正確的等位移多采樣值。有：t1=t0．2－t0． 1，t2=t0．3－t0．2，…。
當硬幣后沿通過E點時，停止采樣，D點和E點的沿幣道方向的距離為y，設通過E點的時刻為tE，則有：

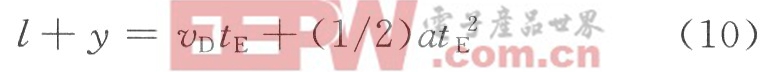
由此即可計算出tE，即為硬幣通過幣道時最后一個采樣點。
根據式(9)，要求得t，涉及到開方運算。開方運算的算法主要有Newton-Raphson算法、SRT-Redun-ant算法和Non-Redudant算法。這三種算法可以得到開方運算的近似結果。關于上述三種算法的介紹參見參考文獻[1―3]。
為了有足夠高的檢測精度，要求t精確到1μs。另外，由于硬幣由C點到D點的最小時間為0．3 ms，所以必須在0．3 ms內完成上述的算法。通過FPGA不難實現這些要求，但是若采用單片機來實現就有一定的難度，如：若用51單片機，頻率12 MHz來實現，則機器周期就是1μs，要實現上述算法是不可能的。所以在該設計中采用FPGA實現。
2．5 基于FPGA的多倍周期同步測頻法
在該設計中，檢測線圈為電渦流反射式互補檢測，準確地測試出其輸出頻率是很重要的。對于頻率的測試，有測頻法、測周期法，但測量精度都不夠高，在該設計中，兩種測試方法誤差都比較大，所以采用等精度多倍周期同步測頻法，可達到較高的精度。
由于硬幣通過檢測線圈時的速度范圍為：0．1～0．5 m／s，要求每隔0．1 mm距離采樣一次，則采樣的時間間隔范圍為0．2～1ms。為了保證采樣的快速和準確性，采樣時間不能超過0．2 ms，本設計采樣時間取0．1 ms。
該設計中，FPGA的頻率為100 MHz，由檢測線圈及檢測電路組成的振蕩器頻率為200 kHz(此頻率指硬幣未通過線圈時的振蕩頻率)。
所謂測頻法，就是先給定一個閘門時間，在此閘門時間內，對被測頻率信號計數，由此即可計算出被測信號的頻率。在本設計中，閘門時間為0．1 ms，被測信號頻率為200 kHz左右，若用測頻法，則測量誤差為：
1／(0．1×10-3×200×103)=5％
所謂測周期法，就是在被測頻率信號的一個周期內，對參考頻率信號進行計數，由此即可計算出被測信號的周期，在本設計中，參考頻率信號為100 MHz，被測信號頻率為200 kHz左右，若用測周期法，則測量誤差為：
(200×103)／(100×106)=0．2％
由此可見，都有較大的誤差，下面用等精度多倍周期同步測頻法，既可以在振蕩頻率變化的情況下保持精度的一致，又可以減少測量誤差，提高測試精度。
設被測信號頻率為fx，計數器CT1對fx進行計數；參考信號頻率為fr，計數器CT2對fr進行計數。
CT1的閘門開放時間完全與fx的m個周期同步。閘門開放時間T1=mtx。在fx的第一個上升沿和第m+1個上升沿之間的mtx時間間隔內，允許CT2對fr計數，計數值記為N。上述測頻的時序圖如圖7所示。

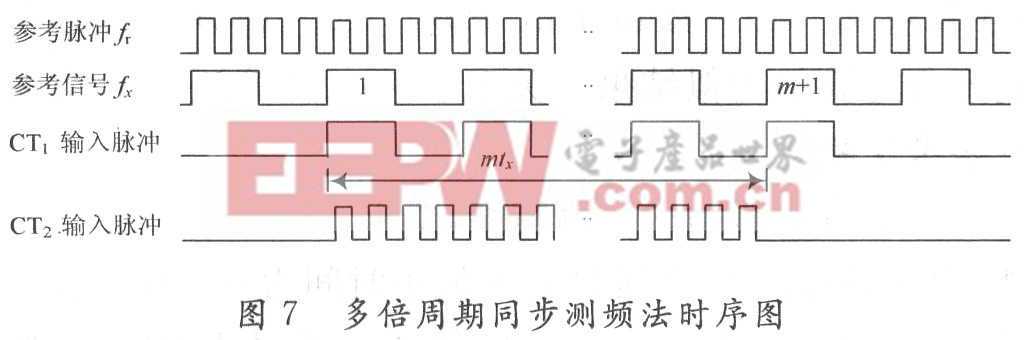
fx的計算公式如下：
fx=m/Nfr