基于FPGA的正交數字混頻器中數控振蕩器的設計與實

要CORDIC(COordination Rotation DIgital Computer)算法實現正交數字混頻器中的數控振蕩器的方法。首先推導了算法產生正余弦信號的實現過程,然后給出了在中設計數控振蕩器的頂層電路結構,并根據算法特點在設計中引入流水線結構設計。

CORDIC算法;

/余弦信號正交特性好等特點。而且的相位、幅度均已數字化,可以直接進行高精度的數字調制解調。隨著數字通信技術的發展,傳送的數據速率越來越高。如何得到一個可數控的高頻載波信號是實現高速數字通信系統必須解決的問題。本文將介紹如何在中實現高速正交數字混頻器中的數控振蕩器設計。

1NCO的頂層電路結構

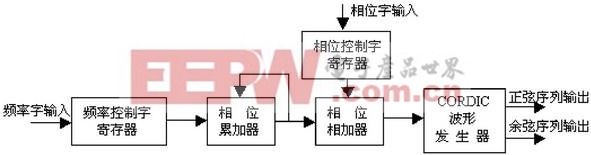
2CORDIC迭代算法的流水線結構

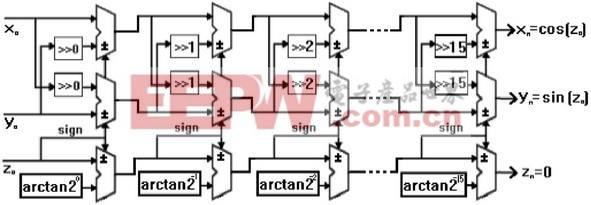
3NCO的部分仿真時序圖

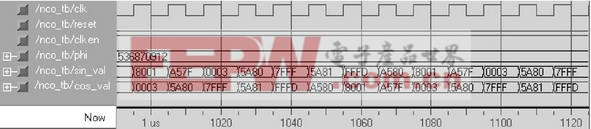
, 傳統做法是采用查表法,即事先根據各個正余弦波相位計算好相位的正余弦值,并按相位角度作為地址在存儲器中對其進行尋址,構成一個幅度相位轉換電路即波形存儲器,通過該轉換電路進行查表獲得正余弦信號樣本。為了提高數控振蕩器的頻率分辨率,往往需要擴大波形存儲器的容量,造成存儲資源的大量消耗。而且,如果需要外掛來存儲波形,由于受到讀取速度的影響,數控振蕩器的輸出速率必然受到制約。因此,當設計高速、高精度的數控振蕩器時,查表法就不適合采用

/余弦樣本。基于矢量旋轉的算法正好滿足了這一需求該算法有線性的收斂域和序列的特性,只要迭代次數足夠,即可保證結果有足夠的精度。統一的形式的基本原理是,初始向量1(x,y)旋轉角度V(x,y):

2=xcos1sin

2=ycos1sin (1)

2=(x-ytancos

2=(y+xtancos

2的整數次冪,即：-i)+1表示逆時針旋轉,表示順時針旋轉,故第步旋轉可用K表示,以字長為例,則為了抵消迭代對比例因子的影響,可將每級迭代的輸入數據、校正后再參與運算,以避免在迭代運算中增加校正運算,降低算法的速度。