基于CORDIC算法的OFDM 系統載波同步實現
加入技術交流群
在接收端，通過對訓練序列的延遲相關，可以得到如下公式：
然后對上式求相角，可以得到：
如果|ψ|的值能夠保證小于π，那么，其頻偏估計值為：
對于載波頻率偏移的計算與補償，一般需要實現的兩個最重要的功能：第一是求相角的功能，第二是需要產生糾正頻偏用的和函數。求相角函數的實現有許多可行的方法。其中最直觀的就是通過復數虛部對實部的比值，也就是求反正切來得到角度值。這樣就引入了除法運算，并且需要在RAM里建立一個反正切函數的查找表。另一種方法是使用CORDIC算法，該算法在多次迭代的情況下，只需要很少的硬件資源，但由于迭代計算的特點，所以會有幾個時鐘周期的時延。由于相角的計算在每一個幀到來時只需要計算一次，所以，這個很小的時延不會對系統的性能造成影響。由于采用查找表的方法計算反正切函數需要大量的RAM空間，所以，設計時可采用CORDIC算法來實現角度的計算。本文引用地址：http://www.104case.com/article/191868.htm
3 CORDIC算法原理與FPGA實現
3．1 CORDIC算法
計算三角函數和其它一些硬件不易實現的函數，一般可使用查表法、多項式展開或近似的方法。這些方法均不能兼顧速度、精度、簡單性等方面的要求。CORDIC算法則是為解決這種問題而產生的。它從算法本身人手，可將復雜的算法分解成一些在硬件中容易實現的基本算法，如加法、移位等，從而使這些算法在硬件上可以得到較好的實現。由于該算法是一種規則化的算法，它滿足硬件對算法的模塊化、規則化要求，因此，CORDIC算法是可以充分發揮硬件優勢并利用硬件資源來實現硬件與算法相結合的一種優化方案。
3．2 用于頻偏校正的CORDIC算法的旋轉模式
假設直角坐標系內有一個向量a(xa，ya)，逆時針旋轉θ角度后得到另一個向量b(xb，yb)，那么，這個過程可以表示為：
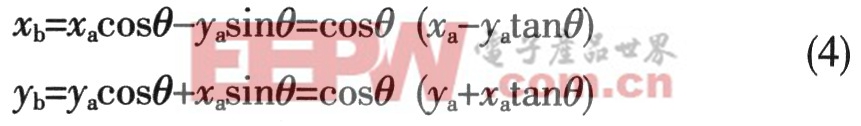
如果向量a(xa,ya)經過n次旋轉才到達向量b(xb，yb)，其中第i次旋轉的角度為θi，那么，第i次旋轉的表達式為：
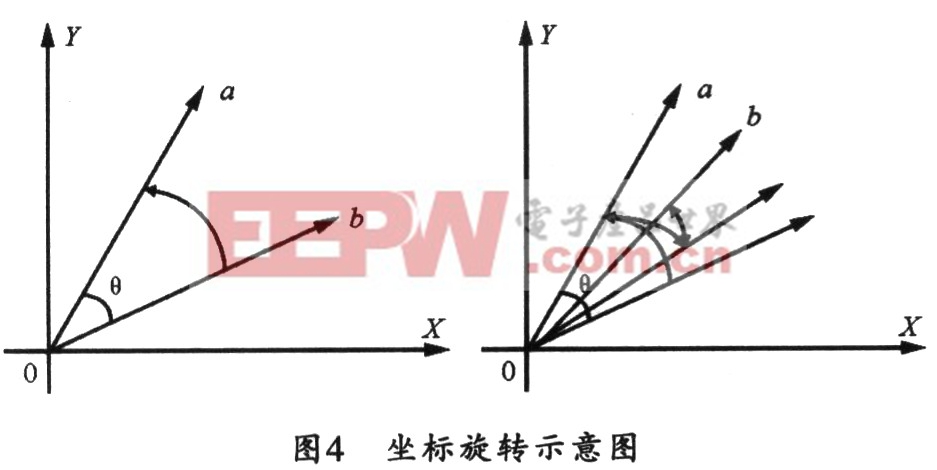
CORDIC算法的旋轉示意圖如圖4所示。圖中，
若取旋轉的角度總和
這里的Si={-1；+1}。其中Si=+1表示向量是逆時針旋轉，Si=-1表示向量是順時針旋轉。式中：
隨著旋轉次數的增加，該式將收斂為一個常數k：
如果暫時不考慮這個增益因子k，則有：
這就是CORDIC的迭代式，它只需要通過移位和相加就可以完成矢量的旋轉。其向量a向向量b逼近的精度由迭代的次數決定，迭代的次數越多，逼近的精度越高。而引入變量z則表示進行i次旋轉后與目標角度之差。這樣，迭代n次所得到的最終結果為：
可以看出，此模式下，便可求出給定角度的三角函數值。
評論