基于FPGA的復數浮點協方差矩陣實現

O 引言
協方差矩陣的計算是信號處理領域的典型運算，是實現多級嵌套維納濾波器、空間譜估計、相干源個數估計以及仿射不變量模式識別的關鍵部分，廣泛應用于雷達、聲吶、數字圖像處理等領域。采用FPGA(Field Programmable Gate Array)可以提高該類數字信號處理運算的實時性，是算法工程化的重要環節。但是FPGA不適宜對浮點數的處理，對復雜的不規則計算開發起來也比較困難。故目前國內外協方差運算的
FPGA實現都是采用定點運算方式。
在所有運算都是定點運算的情況下，每次乘法之后數據位寬都要擴大一倍。若相乘后的數據繼續做加減運算，為了保證數據不溢出，還必須將數據位寬擴展一位，而協方差矩陣的運算核心就是乘累加單元，隨著采樣點數的增加，位寬擴展呈線性增加。最終導致FPGA器件資源枯竭，無法實現設計。為了保證算法的實現，必須對中間運算數據進行截斷，將每次累加的結果除2(可以通過移位運算來實現)，以避免溢出。
此外，在應用MUSIC算法時，各種計算都是復數運算。為達到減少算法的計算量，提高MUSIC算法處理速度的目的，許多文獻致力于研究陣列的結構特點，在保證測角精度的前提下，尋找一種簡單而有效的數據預處理方法，將復數矩陣轉化為實數矩陣，把復矢量用一個實矢量來代替，從而將復數運算轉化為實數運算。
接收陣元模型可分為任意離散陣、均勻圓弧陣、均勻圓陣和均勻線陣。在實際應用中，比較常見的是均勻線陣和均勻圓陣。每種陣列模型都有各自的特點，加之陣元數目的取值不同，也會導致陣列流型的對稱性變化。針對不同的陣元模型和陣元數，數據預處理的方法也會有所不同。
對于數據預處理的研究，目前已經有了一些比較成熟的算法。對于一個偶數陣元的對稱陣列(包括均勻線陣和均勻圓陣)，相關研究表明，可利用其對稱性，分成兩個完全對稱的子陣，選擇合適的參考點，構造互為共軛對稱的方向矩陣，進而構造一個線性變換矩陣，即可達到將復數矩陣轉化為實數矩陣的目的。
對于奇數陣元的均勻線陣，也有相關研究成果表明，通過構造一個酉矩陣，也可以達到數據預處理的目的。
由于均勻圓陣的陣列流型矩陣不是Vandermonde矩陣，即不具備旋轉不變性，因此適用于奇數陣元的均勻線陣的預處理理論不能直接用于奇數陣元的均勻圓陣，需要將圓陣先轉換到模式空間——虛擬線陣，而轉換需要第一類Bessel函數，不適宜用硬件實現。
以上研究表明，目前除了奇數陣元的均勻圓陣外，其他常用陣列模型都可以通過預處理的方法將復數運算轉換為實數運算。若在某些特定的情況下，必須采用奇數陣元的均勻圓陣。此時，基于復數運算的協方差矩陣的實現就成為一種必然。
因此，在充分應用FPGA并行處理能力的同時，為了擴展數據處理的動態范圍，減少數據溢出機率，避免數據截斷所產生的誤差，提高協方差矩陣的運算精度以及擴展該運算的通用性。本文以空間譜估計作為研究背景，研究了復數據運算和浮點運算的特點，提出了一種適用于任何陣列流型、任意陣元的基于復數浮點運算的協方差矩陣的FPGA實現方案。

1 求解復數浮點協方差矩陣
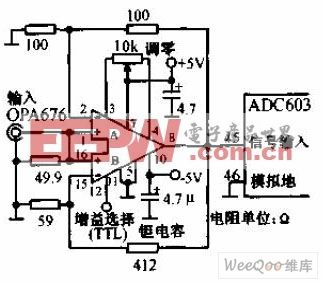
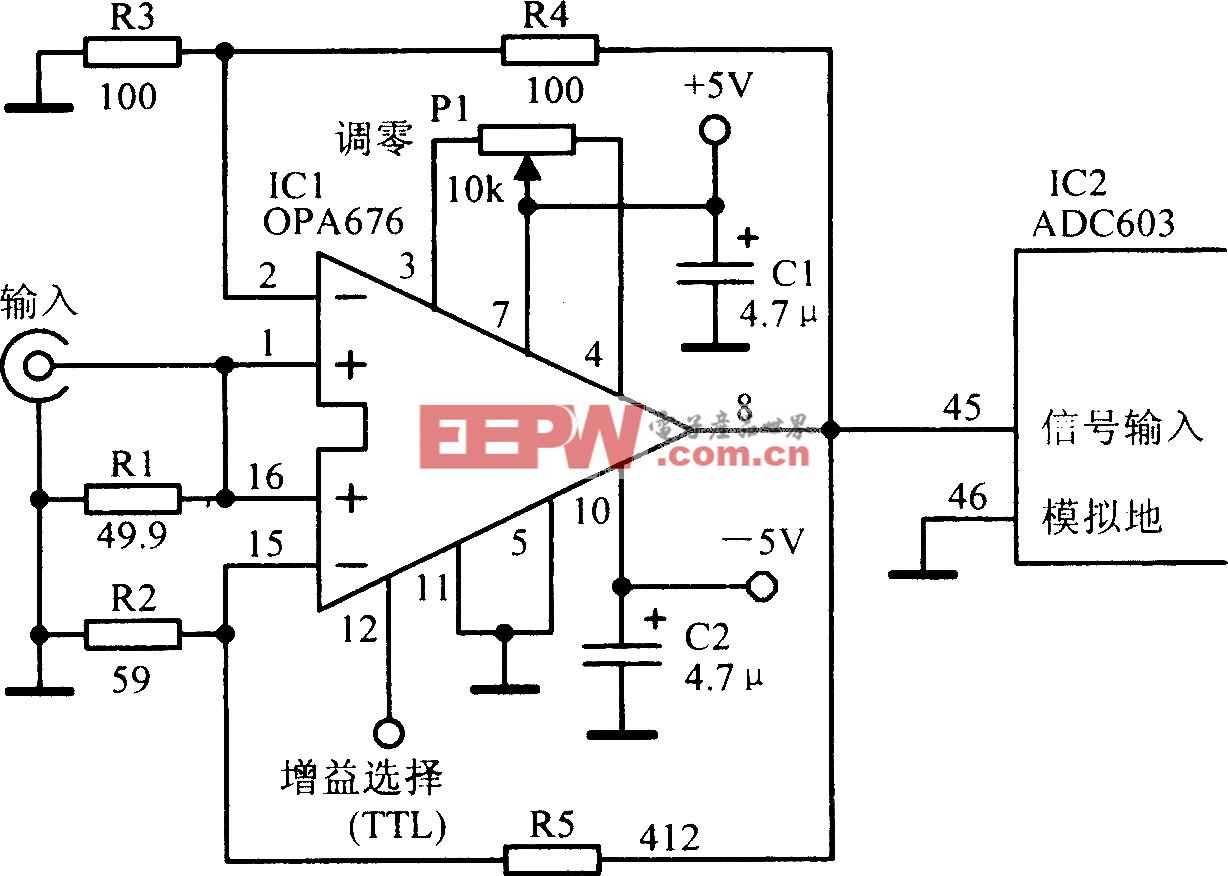
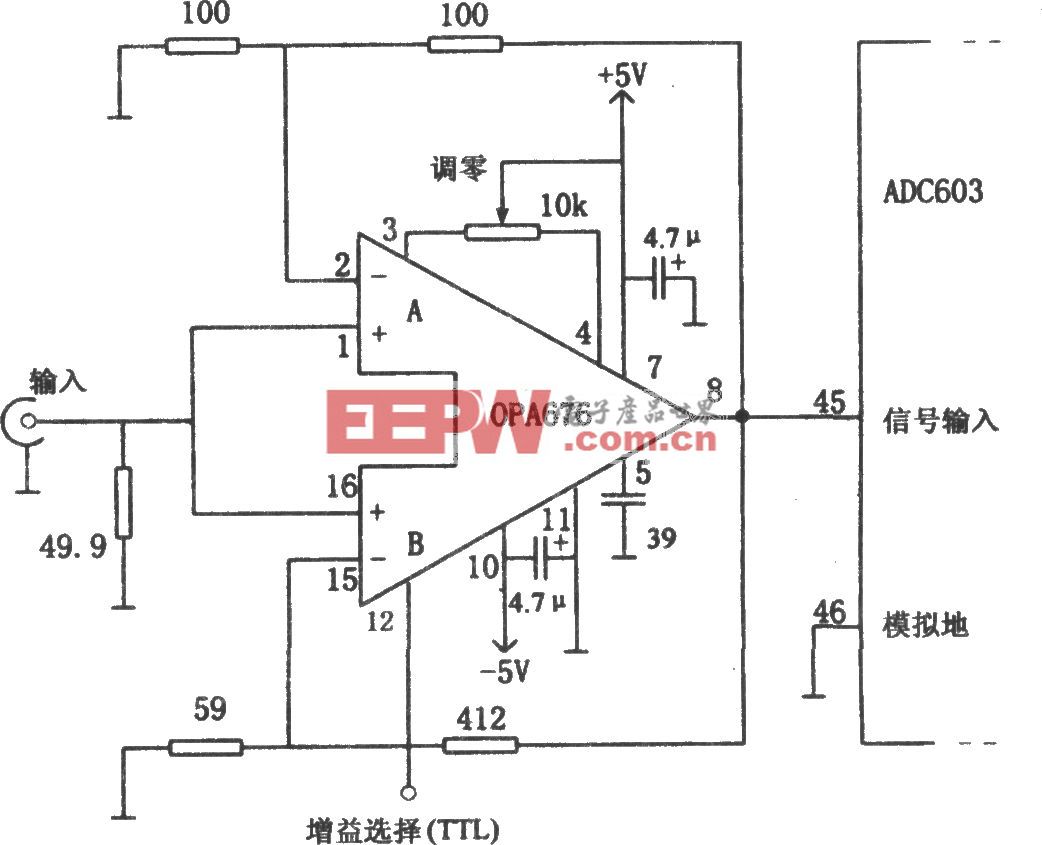
以11陣元的均勻圓陣為例，其協方差矩陣的求解方案原理框圖如圖1所示。

1．1 FIF0數據緩存器
在該設計方案中選擇FIFO作為數據存儲器，這是因為一旦多路接收機有數據輸出，就會啟動FIFO進行存儲，進而FIFO的不空信號有效(empty=O)，觸發后續的矩陣運算；否則，運算停止，一切狀態清零，FPGA恢復idle(空閑)狀態，等待新的快拍采樣數據的到來。
這樣可以很方便地控制運算的開始和結束。矩陣運算所需要的同步時鐘需要設計一個類似于單穩態觸發器的模塊。當檢測到empty=‘0’時，就觸發一個含有121個clk(對于串行方案而言)時鐘信號周期長度的高電平。該高電平與主時鐘相與便可以得到運算的同步時鐘。
1．2 數據共軛轉換
由于測向陣列的輸出矢量X(t)是一個復矢量，對其求協方差矩陣需用陣列輸出列矢量X(t)與其共軛轉置矢量XH(n)對應相乘。如式(1)所示：

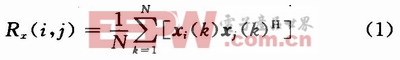
1．3 定點數到浮點數的轉換
定點計算在硬件上實現簡單，計算速度比浮點計算要快，但是表示操作數的動態范圍受到限制，浮點數計算硬件實現比較困難；一次計算花費的時間也遠大于定點計算的花費，但是其表示的操作數動態范圍大，精度高。在本設計中，考慮到系統的數據動態范圍和運算精度，選擇浮點計算。由于運算數據是直接從接收機I，Q兩路通道的A／D變換器的輸出獲得，為定點數，因此必須要有一個將A／D采樣的定點數據轉換為浮點數的過程。設計中將16位定點數轉換為IEEE 754標準的單精度格式。32位單精度格式如圖2所示，最高位為符號位，其后8位為指數e(用移碼表示，基數f=2，偏移量為127)，余下的23位為尾數m。