基于FPGA的24×24位低功耗乘法器的設計

O 引言
乘法器被廣泛應用于各種數字電路系統中，如DSP、數字圖像處理等系統。隨著便攜電予設備的普及，系統的集成度越來越高，這也對產品的功耗及芯片的散熱提出了更高的要求。本文提出了一種新的編碼算法，通過這種算法實現的乘法器可以進一步降低功耗，從而降低整個電子系統的功耗。

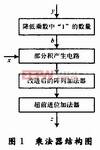
1 乘法器結構
本文介紹的24×24位乘法器的基本結構如圖1所示。其中，“降低乘數中‘1’的數量”實現對乘數y的編碼，以降低乘數y中“1”的數量，這可以在“部分積產生電路”中降低部分積的數量，“部分積產生電路”產生的部分積在“改進后的陣列加法器”和“超前進位加法器”中相加，最后得到乘積z。

2 降低部分積數量的編碼算法
設x，y是被乘數和乘數，它們分別用24位二進制數表示，最高位是符號位，z是乘積，用47位二進制表示，最高位是符號位，“1”表示負數，“0”表示正數。則它們的關系可以用下式表示：


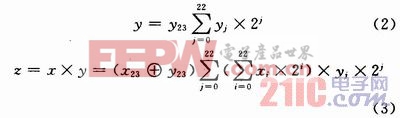
式中：xi，yi分別是x，y的權位。如果按式(3)進行乘法計算，需要將與所有的yi相乘，產生23行部分積，然后再將其相加，即使yi=0，也要進行上述運算，這樣就勢必增加乘法器的功耗和延時，因此，在下面將會對全加器和半加器進行改進，使僅與yi=1相乘，從而避免與yi=0相乘。首先介紹降低乘數y中“1”的數量的編碼算法。用一個事例說明本文介紹的算法的優越性。設m1，m2分別是乘數和被乘數，且令m1=01110111，如果用m2與m1中的每一位相乘，則會產生6個m2和2個“0”列，如果按照Sanjiv Kumar Mangal和 R． M． Patrikar所建議的方法，則：
01110111(m1)=10001000(n1)-00010001(n2) (4)
將m2分別與n1和n2相乘，再將它們的乘積相減即得乘積結果。但是，在這一過程中，一共產生4個m2。如果按照本文所建議的方法，會進一步降低m2的數量，即：
01110111(m1)=10000000(n1)-00001001(n2) (5)
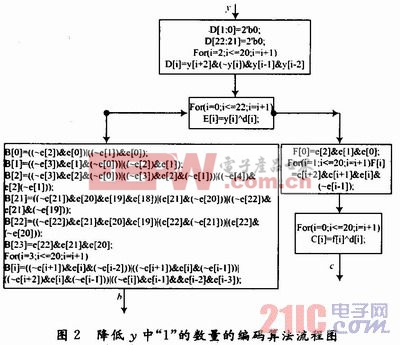
由式(5)可以看出，n1和n2中共有3個“1”，因此，可以進一步降低部分積的數量。當乘數的位數較大時，本文提出的算法優越性更大。具體編碼流程如圖2所示。

3 部分積的產生及相加
在數字電路中，功耗主要由3部分構成，即：