FIR濾波器的FPGA實現方法

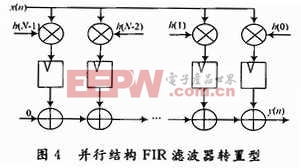
基于并行結構的轉置型FIR濾波器實現了數據的并行輸入，在1個周期內就能完成1次濾波，并且各級結構相同，在每個階段都可以讀出數據，可以對濾波階數進行擴展或者縮減，實現任意階數的濾波器。但是由于基于的是并行結構，便有著并行結構的一些缺點，主要是對于高階的濾波器，其資源占用量是巨大的，設計成本高。雖然這樣，轉置型FIR濾波器仍是應用廣泛的一種濾波器。
2．4 基于FFT的結構
應用快速傅里葉變換(fast fourier transform，FFT)實現FIR濾波器是一種快速實現濾波算法的重要途徑。由式(1)可知，FIR濾波器的輸出y(n)是輸入x(n)與系統沖擊響應序列h(n)的卷積，應用FFT可以快速實現卷積變換。如圖5所示，先將輸入信號x(n)通過FFT變換為它的頻譜采樣值X(k)，然后再與FIR濾波器的頻響采樣值H(k)相乘，H(k)可事先存放在存儲器中，最后再將乘積X(k)H(k)通過快速傅里葉反變換(IF-FT)還原為時域序列，即得到輸出y(n)。

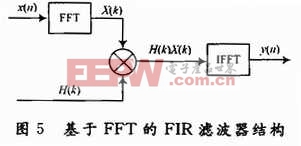
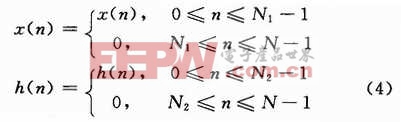
為實現FFT，根據兩有限長序列的線性卷積可用其循環卷積代替而不發生混疊，必須選擇循環卷積長度N≥N1+N2-1，即將x(n)和h(n)補零至長度為N的序列，即：

在基于FFT的FIR濾波器結構中，求X(k)，H(k)以及反傅里葉變換y(n)需要的乘法次數均為N／2log2N，而計算X(k)H(k)需要N次乘法，所以基于FFT的總乘法次數為mf=3／2Nlog2N+N。由于h(n)滿足式(3)條件，所以直接卷積所需的乘法次數為md=1／2N1N2。假設N1=N2，則比較這兩種乘法計算量有：

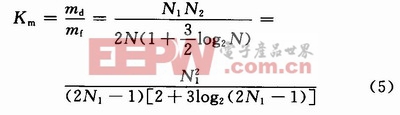
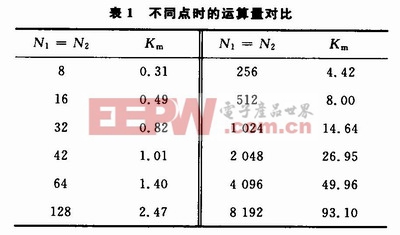
從表1可知，當N142時，FFT法的運算量小于直接卷積的運算量，當N1=42時，FFT法的運算量與直接卷積的運算量相當，當N1>42時，FFT法的運算量大于直接卷積的運算量，并且隨著N1增加，FFT法的運算速度越來越快，特別是N1=8 192時，FFT法的運算速度與直接卷積相比快上將近100倍。

2．5 分布式結構
2．5．1 分布式算法原理
分布式算法(distributed arithmetic，DA)于1973年就由Croisier提出，但是直到FPGA出現，才廣泛的被應用于FPGA中計算乘累積和。