一種基于FPGA的真隨機數發生器設計與實現
1.4 隨機源模塊的電路設計
各個振蕩器的輸出經過異或運算可以增加隨機性,而亞穩態的傳播會造成后續電路的錯誤動作,因此使用同步器將異或后的隨機序列與后續電路隔離開來,同時也方便采集穩定的輸出序列做性能分析。此處采用了三級寄存器的同步結構,由MTBF(Mean Time Between Failure)的定義可知,平均需要經過數百年時間才會發生一次亞穩態通過同步器向下傳播的事件,因此是滿足設計要求的。該模塊電路圖如圖4所示。本文引用地址:http://www.104case.com/article/190794.htm
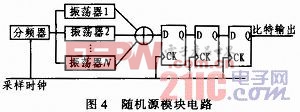
1.5 后續處理模塊的設計
理想情況下,D觸發器所采集的信號具有隨機的統計特性,可是FPGA內部電路不可避免地會受到溫度漂移、電壓抖動等不良因素影響,從而導致采樣得到的隨機信號中存在偏置,影響結果的統計特性。所以在采樣得到隨機序列后要對數據進行消偏處理,使0和1出現的概率相當。
本設計采用16位最大長度二進制偽隨機序列(Pseudo Random Binary Sequence)的輸出與采樣得到的隨機序列進行異或運算作為后續處理,PRBS產生電路消耗資源少并且使用線性反饋移位寄存器實現,非常適合于在FPGA上實現。它的生成多項式是:
![]()
多項式表示如圖5所示。

2 TRNG的FPGA實現與測試
整個TRNG的實驗環境由外部時鐘源、FPGA開發板以及邏輯分析儀組成。TRNG采用Xilinx公司的Virtex-5系列中的XC5VLX110作為物理實現平臺,外部時鐘頻率為64 MHz。由FPGA產生的隨機數據,經邏輯分析儀采集后,使用DIEHARD battery of tests of randomness隨機數測試程序進行測試,檢驗隨機序列的性能。
DIEHARD測試是由16項測試組成的用來度量隨機數發生器性能的一組統計學測試,它由George Marsaglia開發并于1995年首次發布。DIE HARD的測試結果叫做P-value,它由方程P-value=Fi(X)計算得到,其中Fi試圖建立樣本X在0和1間服從均勻分布的分布函數。因為Fi是漸進逼近的,它在尾部的近似效果變差,所以數值接近0或1的P-value在真隨機序列中極少出現。當被測序列隨機性能很差時,會有很多P-value的值是精確到小數點后數位的0或者1,例如1.000 000。需要強調的是,P-value等于1.000 000或0.000000是序列為真隨機序列的充分不必要條件。
2.1 FPGA位置約束
為保證每個振蕩器中的兩個獨立振蕩環的理論振蕩周期相同,以便更容易在鎖定期間產生亞穩態,加大噪聲對輸出電平的影響,同時盡量讓各個振蕩器的輸出在進行異或運算前延遲不出現太大偏差。所以對TRNG中的振蕩環進行位置約束:將振蕩環中的反相器約束在左右相鄰的邏輯單元(Slice)中,讓各個振蕩環分別約束在上下相鄰的邏輯單元中。
2.2 振蕩器數目對統計特性的影響
在32 MHz的采樣頻率下,分別以15組、19組、27組和32組振蕩器作為TRNG的隨機源,隨機序列經過同步器后不與PRBS運算直接輸出。將采集到的隨機序列送入測試程序進行測試以后,其結果如表1所示。
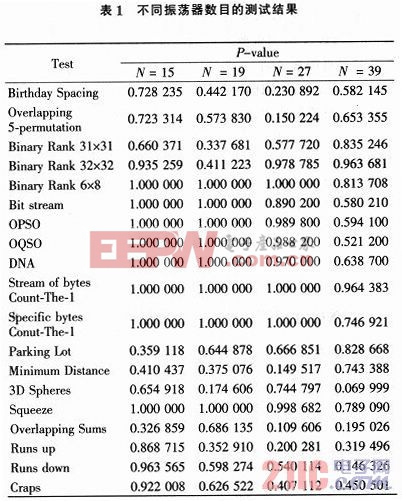
可以看出,振蕩器的數目直接影響隨機源模塊產生序列的統計性能,振蕩器數目越多,TRNG輸出序列的隨機性越好。但是如果振蕩器的數目太多,會消耗過多的硬件資源,功耗也過大。因此,不宜通過單純地增加振蕩器數目的方法提高隨機序列的性能。















評論