基于FPGA的數字三相鎖相環(huán)優(yōu)化設計
加入技術交流群
3 三相鎖相環(huán)
的FPGA設計3．1 未優(yōu)化的三相鎖相環(huán)
的FPGA結構根據圖1三相鎖相環(huán)
的拓撲結構及原理，三相鎖相環(huán)的基本硬件結構如圖3所示。首先通過采樣，將三相電壓離散化并處理為32 b有符號數，經過Clarke變換與相應的參數相乘后相加得到兩相靜止坐標的分量μα，μβ。共有5個乘法運算，3個加法運算。然后是Park變換，在此三相鎖相環(huán)
中只需要μq分量，需要2個乘法運算，2個三角函數計算，1個加法運算。后面的PI控制器需要2個乘法運算，2個加法運算。最后是VCO需要2個加法運算。整個運算過程共需要9個乘法運算，9個加法運算，2個三角函數運算。從對三相鎖相環(huán)的基本結構分析可知，整個過程需要9個乘法運算，2個三角函數運算。在FPGA中實現乘法運算和三角函數運算會消耗大量的資源。特別是傳統(tǒng)的查表法三角函數運算在消耗大量資源的同時還存在精度問題。
3．2 三相鎖相環(huán)的優(yōu)化設計
由于該設計采用25 MHz的系統(tǒng)時鐘，而采樣頻率為5 MHz，所以設計的時序余量非常大。依據面積和速度的平衡與互換的基本原則，針對乘法運算多的特點，采用乘法復用，系統(tǒng)中只保留一個乘法模塊，通過合理選擇，達到時分復用。
在Park變換中存在的三角函數運算，可以通過CORDIC算法優(yōu)化。CORDIC算法是通過基本的加法和移位運算來代替乘法和三角函數運算的，特別適合矢量旋轉的運算。使用迭代的方法，多步完成要旋轉的角度。CORDIC算法可以實現如式(6)所示的運算。
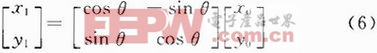
式中：x0，x1為初始坐標；θ為要旋轉角度；y0，y1為最終的坐標。通過對式(6)的分析與Park變換相比較可以發(fā)現，只要把角度取負，就可以通過CORDIC算法完成整個Park變換的運算。
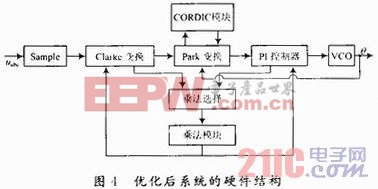
優(yōu)化后系統(tǒng)的硬件結構如圖4所示。本文引用地址：http://www.104case.com/article/189839.htm
4 結語
本文分析了三相鎖相環(huán)的基本原理。針對FPGA的特點對鎖相環(huán)進行了優(yōu)化設計，并利用Verilog HDL硬件描述語言編碼實現。該設計可直接用于PWM整流器、UPS等控制系統(tǒng)中。
fpga相關文章:fpga是什么
鎖相環(huán)相關文章:鎖相環(huán)原理
評論