高階濾波器的設計

實現高階濾波器的方法是把基高階函數分解成多個二階因式之積，每個二階因式用對應的二階濾波器來實現，將這些二階濾波器串接起來即是所需的高階濾波器。這樣，就把設計復雜的高階濾波器的問題簡化為二階節基本單元設計。

設計舉例：

例如，設計截止頻率為1000HZ的低通濾波器，要求通帶幅頻響應平坦。截止頻率以外的下降率為100DB/10倍頻。

顯然，選擇五階巴特沃斯LPF，其框圖如圖5.4-59A所示。由一級和兩級二階電路組成。巴特沃斯型網絡參數見表5.4-5。

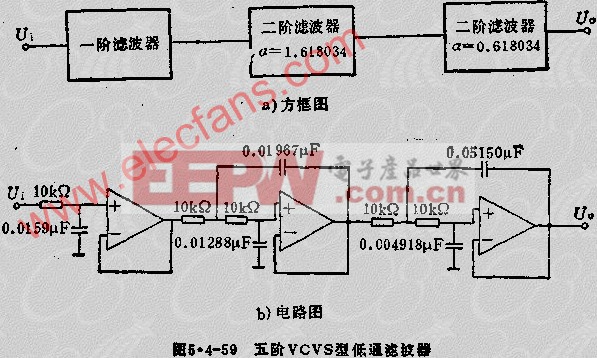
1）已知條件WO、A和HO的確定，由表5.4-5查得N=5時有WO=WO1=WO2=WO3=1.000000。A2=1.618034，A3=0.618034。

選擇HO=1

這里，頻率已經歸一化。由此可求得各級實際截止頻率為

WC=WO=WO1=WO2=WO3=2πFC=6280/S

對巴特沃斯LPF有WC和WO相等

2）確定電路形式及計算各級R和C的數值

既可選擇VCVS型LPF，也可選擇MFB型的LPF的具體電路來實現設計的要求。

本例選擇VCVS型的LPF。

在計算R和C的數值時，既可先任選定C，也可先任選定R。本例選定各級RC網絡中的R均等于10K。

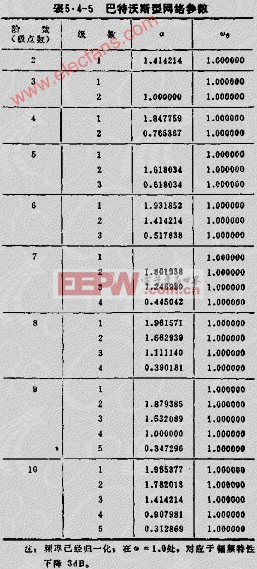
第一級的已知條件是WO=6.28/NS，R=10K，HO=1。即可求出此級C=0.0159UF。

第二級的已知條件是WO=6.28/NS，A2=1.618034，HO=1，R=10K。代入式（見下式），即可求出此級的C3=0.01967UF，C4=0.01288UF。

第三級的已知條件是WO=6.28/，A8=0.618034，HO=1，R=10K。代入式：

即可求出第三級的C2=0.05150UF，C4=0.004918UF。

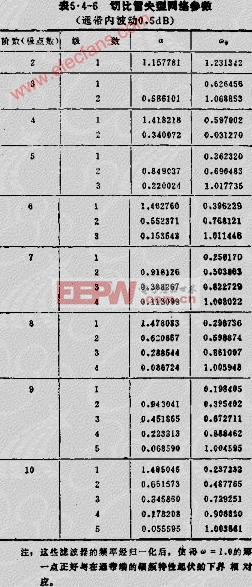
由此則設計出如圖5.4-59B所示的VCVS型五階LPF。表5.4-6~表5.4-10示出了切比雪夫和貝塞爾網絡參數。

在實際應用中，要求能快速、簡便的設計或選用具有一定精度，能滿足工程上要求的濾波器。因而在工程上，都采用直接查表法設計所需的濾波器。

制作有源濾波器時，設計者要選用在GB積和SR均能滿足要求的運算放大器。一般要求FCGB/50，對截止頻率和中心頻率高的濾波器應選用SR大的集成運放。特別是在高通濾波器中，往往由于SR不夠高，會產生嚴重波形失真，或者Q值下降。再者，電路中的無源元件的變化對電路的靈敏度有很大影響，因此對低階濾波器，要求電阻容差為5%，對五階和六階要求電阻容差為2%，對七階和八階要求電阻容差為1%。對電容，因價格的問題，在低階情況下，要求其容差為10%即可，對更高階次，當然選用和電阻相當容差是令人滿意的。但是要求應適當放寬。另外，還對運放噪聲等指標，有一定的要求。

在設計出一個有源濾波器的實際電路以后，還需進行最后的調整。即調整元件的數值和增益，以補償元件的公差和寄生效應。

密Q值濾波器

前面所求的濾波器都不適合于實現高Q值網絡函數。實現高Q值的電路，在電路結構上的復雜性大大地增加了。如圖5.4-60所示的是一雙二次型二階低通濾波器，其Q值可高達100。至于其他高Q值電路。