LMS自適應濾波器干擾方法

摘要 自適應濾波器能有效地提高雷達在復雜電磁環境下的適應能力，在雷達信號處理機中得到廣泛的運用，其核心是使用自適應算法，將濾波器設計成根據目標對照射信號的響應，及外界的電磁環境的變化等因素，調節濾波器的自身結構參數，最終趨于穩態的維納濾波器，實現對目標的最優檢測。文中主要分析LMS自適應算法中存在的步長固定等缺點，設計干擾信號，并用計算機仿真驗證其對LMS濾波器的干擾效果，該干擾信號可使自適應濾波器無法實現結構上的自動優化，降低其雷達的工作效能。
關鍵詞 自適應濾波器；干擾；雷達對抗；LMS

隨著科學技術的發展，雷達系統結構的發展也趨于對外界響應的自適應，其內部結構有越來越多的可變參數器件，主要根據目標對照射信號的響應、外界的電磁環境變化等各種因素，調節自身的結構，實現對目標的最優檢測。由于自適應濾波器的輸入信號和噪聲統計特性在一定情況下可實時變化，系統參數也同時做出相應的動態調整，這種結構上各參數的調整優化可以通過自適應算法得以實現，LMS算法是自適應濾波算法中較為重要的算法。因此有必要尋找這類算法的缺點，研究對其干擾的方式，使之無法實現結構上的自動優化，降低雷達的工作效能。

1 LMS自適應濾波原理和分析
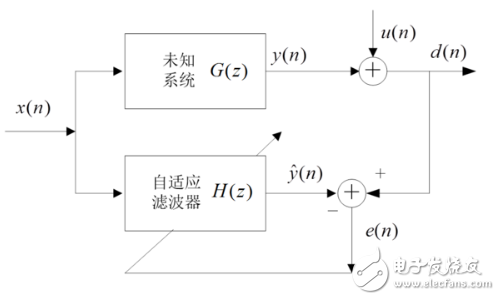
自適應濾波器有兩個關鍵概念，一是收斂后得到穩定的最優解為一個維納濾波器，二是自適應算法引入負反饋控制結構中可調參數向維納解不斷逼近。維納濾波器是以最小均方誤差為準則的濾波器。其核心為維納霍夫方程
[Фxs]=[Фxx][h] (1)
其中，Фxs是有用信號S和外界混入噪聲的有用信號兩者之間的互相關矩陣。Фxx是外界輸入信號的自相關矩陣。h是濾波器的系數，由式可得濾波器的系數表達式為
[h]=[Фxx]-1[Фxs] (2)
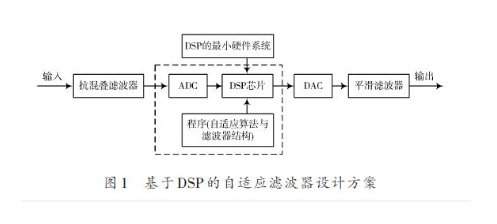
典型的基于LMS算法的自適應濾波器結構如圖1所示。

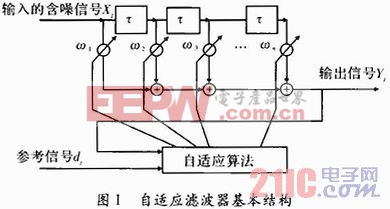
LMS濾波器是基于最小均方誤差準則的自適應濾波器，輸入的含噪信號為Xj，參考信號為dj，兩者間的均方誤差公式為

經過一段時間后，最終可得到最優權值的濾波器系數，為一個維納濾波器，即式(2)。同時均方誤差也達到最小狀態

其中，W*T為最佳權矢量。